Campana de Gauss: Descubre cómo esta función matemática te ayuda a comprender la distribución de datos de manera sorprendente

La Campana de Gauss es una función matemática que se utiliza ampliamente en estadística y probabilidad para describir la distribución de datos. También conocida como curva normal, esta campana es simétrica y tiene una forma característica en la que los valores se agrupan alrededor de un punto central y disminuyen hacia los extremos. Exploraremos cómo funciona la Campana de Gauss y cómo se aplica en diferentes campos, desde la física hasta el análisis de datos.

Comenzaremos explicando los conceptos básicos de la Campana de Gauss, incluyendo su fórmula matemática y las propiedades clave. Luego, veremos cómo esta función se utiliza para describir la distribución de datos reales y cómo puede ayudarnos a comprender patrones y tendencias en conjuntos de datos. También exploraremos algunas aplicaciones prácticas de la Campana de Gauss, como la predicción de resultados en pruebas científicas y el desarrollo de modelos estadísticos. Además, discutiremos los límites y las limitaciones de esta función y cómo se relaciona con otros conceptos estadísticos importantes. A lo largo del artículo, utilizaremos ejemplos claros para ilustrar los conceptos y facilitar la comprensión de la Campana de Gauss y su importancia en la ciencia y la estadística.

Qué es la campana de Gauss y cómo se representa matemáticamente

La campana de Gauss, también conocida como distribución normal o curva de Gauss, es una función matemática que se utiliza para describir la distribución de datos en una variedad de fenómenos naturales y sociales. Esta función lleva el nombre del matemático alemán Carl Friedrich Gauss, quien la desarrolló en el siglo XIX.

Matemáticamente, la campana de Gauss se define mediante la siguiente ecuación:

f(x) = (1 / (σ * √(2π))) * e^(-(x-μ)^2 / (2σ^2))

Donde:

• f(x) es el valor de la función de densidad de probabilidad en un punto x determinado.
• σ es la desviación estándar de la distribución, que indica qué tan dispersos están los datos alrededor de la media.
• μ es la media de la distribución, que representa el valor central o más probable.
• e es la base del logaritmo natural, aproximadamente igual a 2.71828.
• π es el valor constante de Pi, aproximadamente igual a 3.14159.

Esta función tiene forma de una curva simétrica, con la media ubicada en el centro y los valores más probables concentrados en esa región. A medida que nos alejamos de la media, la probabilidad de encontrar valores disminuye gradualmente.

La campana de Gauss se utiliza ampliamente en estadística y probabilidad para modelar y analizar datos. Al calcular la probabilidad de que un determinado valor caiga dentro de un intervalo, podemos utilizar la función de densidad de probabilidad de la campana de Gauss.

Cuál es el significado de la campana de Gauss en términos de la distribución de datos

La campana de Gauss, también conocida como función gaussiana o distribución normal, es una función matemática que tiene una forma característica en forma de campana. Esta función es ampliamente utilizada en estadística y probabilidad para describir la distribución de datos en una población.

Esta función se representa matemáticamente con la siguiente fórmula:

f(x) = (1 / (σ * √(2π))) * e^((-1/2) * ((x - μ) / σ)^2)

Donde:

• f(x) es el valor de la función en un punto específico x.
• σ es la desviación estándar, que representa qué tan dispersos están los datos alrededor de la media.
• μ es la media, que representa el valor central de los datos.
• e es la constante matemática de Euler, aproximadamente igual a 2.71828.
• π es la constante matemática pi, aproximadamente igual a 3.14159.

La campana de Gauss es simétrica alrededor de la media, lo que significa que la mitad de los datos se encuentran a cada lado de la media. La amplitud de la campana y su "anchura" dependen de la desviación estándar. Cuando la desviación estándar es pequeña, la campana es más estrecha y alta, lo que indica que los datos están más concentrados alrededor de la media. Por el contrario, cuando la desviación estándar es grande, la campana es más ancha y baja, lo que indica que los datos se encuentran más dispersos.

Además de describir la distribución de datos, la campana de Gauss se utiliza para realizar inferencias estadísticas. Se basa en el concepto de teorema del límite central, que establece que cuando se tienen suficientes observaciones independientes de una población, la distribución de las medias tiende a seguir una forma gaussiana. Esto implica que muchas variables en la naturaleza, como el peso de las personas o la altura de los árboles, siguen una distribución normal.

La campana de Gauss es una herramienta fundamental en la estadística y la probabilidad para comprender cómo se distribuyen los datos en una población. Su forma característica permite analizar y hacer inferencias sobre los datos, así como determinar cómo se espera que se comporten determinadas variables en la naturaleza.

Cómo se utiliza la campana de Gauss para analizar conjuntos de datos

La campana de Gauss es una función matemática que se utiliza ampliamente en diversos campos para analizar la distribución de conjuntos de datos. Esta función, también conocida como distribución normal, es especialmente útil cuando se trabaja con valores continuos y se busca comprender la frecuencia con la que ocurren diferentes valores dentro de un rango determinado.

Para utilizar la campana de Gauss, primero se debe tener un conjunto de datos que se quiera analizar. Este conjunto puede estar formado por cualquier tipo de valor numérico, como edades, puntajes de exámenes, temperaturas registradas, entre otros ejemplos. Una vez que se tiene el conjunto de datos, se procede a calcular la media y la desviación estándar.

La media representa el valor promedio del conjunto de datos, es decir, la suma de todos los valores dividida entre el número total de elementos. Por otro lado, la desviación estándar es una medida de dispersión que indica cuánto se alejan los valores individuales de la media. En otras palabras, mide qué tan spread están los valores alrededor de la media.

Con la media y la desviación estándar calculados, se puede construir la campana de Gauss utilizando una función matemática. Esta función tiene su punto más alto en la media y se va extendiendo hacia ambos lados de manera simétrica. La forma exacta de la campana de Gauss depende de los valores de la media y la desviación estándar.

Cuando se traza la campana de Gauss, se obtiene una curva suave que muestra cómo se distribuyen los datos alrededor de la media. Los valores cercanos a la media tienen una mayor frecuencia y a medida que nos alejamos de la media, la frecuencia disminuye. En general, los valores más alejados tienden a tener una menor probabilidad de ocurrencia.

La campana de Gauss es especialmente útil para analizar conjuntos de datos grandes, ya que permite comprender rápidamente cómo se distribuyen los valores y obtener información valiosa sobre la forma en que están agrupados. Por ejemplo, si se tiene un conjunto de edades de una población, la campana de Gauss puede ayudar a determinar si la mayoría de las edades se concentran en cierto rango o si hay una dispersión más amplia.

Además de su aplicabilidad en el análisis de datos, la campana de Gauss también se utiliza en diferentes áreas como la estadística, la física, la economía y la ingeniería. Esta función matemática ha demostrado ser una herramienta poderosa para comprender y describir fenómenos naturales y sociales con un alto grado de precisión.

La campana de Gauss es una función matemática ampliamente utilizada para analizar conjuntos de datos y comprender su distribución. A través de esta función, es posible obtener información valiosa sobre la frecuencia con la que ocurren diferentes valores dentro del conjunto, así como identificar patrones y tendencias. Si tienes un conjunto de datos que quieras analizar, no dudes en utilizar la campana de Gauss para obtener insights sorprendentes.

Cuáles son las propiedades de la campana de Gauss que la hacen tan útil en estadística

La campana de Gauss, también conocida como la función de distribución normal, es una función matemática que se utiliza para describir la distribución de datos en estadística. Esta función se representa gráficamente como una curva simétrica en forma de campana.

Una de las propiedades más importantes de la campana de Gauss es su forma simétrica. Esto significa que la media, la mediana y la moda de la distribución coinciden, lo que indica que los datos se encuentran centrados alrededor de un valor central. Además, esta función tiene dos puntos de inflexión simétricos respecto a la media.

Otra propiedad clave de la campana de Gauss es su desviación estándar. La distribución normal se encuentra completamente definida por su media y su desviación estándar. La desviación estándar nos indica qué tan dispersos están los datos con respecto a la media. Si la desviación estándar es pequeña, la campana será más estrecha y concentrada alrededor de la media. Por el contrario, si la desviación estándar es grande, la campana será más amplia y los datos estarán más dispersos.

Además, la campana de Gauss presenta la propiedad de ser asintótica. Esto significa que la curva nunca toca el eje X, lo que implica que la probabilidad de que un dato tome un valor exacto en la distribución normal es prácticamente cero. En cambio, los valores de probabilidad se concentran alrededor de la media y disminuyen a medida que nos alejamos de ella.

Otro aspecto importante de la campana de Gauss es la regla empírica, también conocida como regla del 68-95-99.7. Esta regla establece que aproximadamente el 68% de los datos se encuentra dentro de una desviación estándar de la media, el 95% se encuentra dentro de dos desviaciones estándar y el 99.7% se encuentra dentro de tres desviaciones estándar. Esta propiedad es muy útil para comprender cómo se distribuyen los datos en relación con la media.

Cómo se calcula el área bajo la curva de la campana de Gauss

Para calcular el área bajo la curva de la campana de Gauss, debemos utilizar el concepto de integrales definidas. La función de la campana de Gauss está dada por la fórmula:

f(x) = frac{1}{sqrt{2pisigma^2}}e^{-frac{(x-mu)^2}{2sigma^2}}

donde mu es la media y sigma es la desviación estándar de los datos.

El cálculo del área bajo la curva se realiza utilizando la integral definida en un rango determinado. La integral definida de una función f(x) en el intervalo [a, b] se calcula como:

int_{a}^{b} f(x) , dx

En el caso de la campana de Gauss, queremos calcular el área bajo la curva en el rango que va desde menos infinito hasta un valor determinado x. Por lo tanto, la integral definida para calcular el área sería:

int_{-infty}^{x} f(x) , dx

Desafortunadamente, esta integral no puede ser resuelta analíticamente de manera exacta. Sin embargo, existe una aproximación numérica muy utilizada llamada regla de Simpson, que permite obtener una solución bastante precisa. Esta regla consiste en dividir el rango de integración en varios segmentos y aproximar el área bajo la curva dentro de cada segmento utilizando polinomios de segundo grado.

Una vez que se realiza la aproximación numérica mediante la regla de Simpson, se obtiene el área bajo la curva de la campana de Gauss en el rango deseado. Este valor representa la probabilidad acumulada hasta ese punto y nos permite comprender la distribución de datos de manera sorprendente.

Cuáles son los casos en los que se puede aplicar la campana de Gauss en la vida cotidiana

La campana de Gauss, también conocida como la distribución normal, es una función matemática que se utiliza para modelar y comprender la distribución de datos en una variedad de situaciones. Aunque a primera vista puede parecer abstracta y alejada de la vida cotidiana, esta función tiene aplicaciones prácticas en diversos campos.

Análisis de mediciones en ciencias naturales

Una de las áreas donde la campana de Gauss se aplica con frecuencia es en el análisis de mediciones en ciencias naturales. Por ejemplo, al realizar experimentos químicos, físicos o biológicos, es común obtener una serie de mediciones que pueden tener un grado de variabilidad. La campana de Gauss permite analizar y entender cómo se distribuyen estos datos, lo cual es útil para identificar patrones, establecer rangos de referencia y detectar anomalías.

Estadística y predicción

La campana de Gauss también tiene un papel fundamental en la estadística y en la predicción de comportamientos. En estadística, esta función se utiliza para describir distribuciones de probabilidad en poblaciones grandes, ya que muchos fenómenos naturales y sociales siguen un patrón de distribución normal. Además, al aproximarse a una distribución normal, la campana de Gauss permite realizar predicciones sobre futuros eventos o resultados basados en datos previos.

Finanzas y economía

En el ámbito financiero y económico, la campana de Gauss también encuentra aplicaciones. Por ejemplo, en el mercado de valores, los precios de las acciones suelen seguir una distribución normal, lo que permite a los inversores y analistas utilizar la campana de Gauss para evaluar riesgos y tomar decisiones informadas. De manera similar, esta función también se utiliza en el análisis económico para comprender la distribución de variables como el ingreso o el consumo.

Procesos industriales y control de calidad

Otro campo en el que la campana de Gauss encuentra utilidad es en los procesos industriales y en el control de calidad. En la producción de bienes y servicios, es común buscar que los productos cumplan ciertas especificaciones y tolerancias. La campana de Gauss puede ayudar a establecer límites y criterios de aceptación/rechazo basados en las características deseadas de los productos y en cómo se distribuyen las mediciones tomadas durante el proceso de fabricación.

Análisis de datos y aprendizaje automático

Finalmente, en el campo del análisis de datos y el aprendizaje automático, la campana de Gauss es ampliamente utilizada. Al modelar los datos utilizando una distribución normal, es posible realizar diferentes tipos de análisis, como la detección de valores atípicos, la estimación de parámetros desconocidos y la clasificación de nuevos registros en base a patrones previamente observados. Esto resulta fundamental en áreas como la inteligencia artificial y la toma de decisiones basada en datos.

Aunque pueda sonar compleja o alejada de nuestro día a día, la campana de Gauss tiene aplicaciones en muchos aspectos de la vida cotidiana. Esta función matemática nos ayuda a comprender e interpretar la distribución de datos en diversas áreas, desde las ciencias naturales hasta las finanzas y el análisis de datos. Su versatilidad y capacidad para modelar fenómenos hacen que sea una herramienta fundamental en numerosos campos.

Qué información podemos obtener al analizar una distribución de datos utilizando la campana de Gauss

La campana de Gauss, también conocida como la curva normal o la distribución normal, es una función matemática que se utiliza para representar las distribuciones de datos en muchos campos diferentes. Nos ayuda a comprender cómo están distribuidos los datos en un conjunto y proporciona información importante sobre su media, varianza y desviación estándar.

Al analizar una distribución de datos utilizando la campana de Gauss, podemos obtener varias informaciones clave:

1. Forma de la distribución

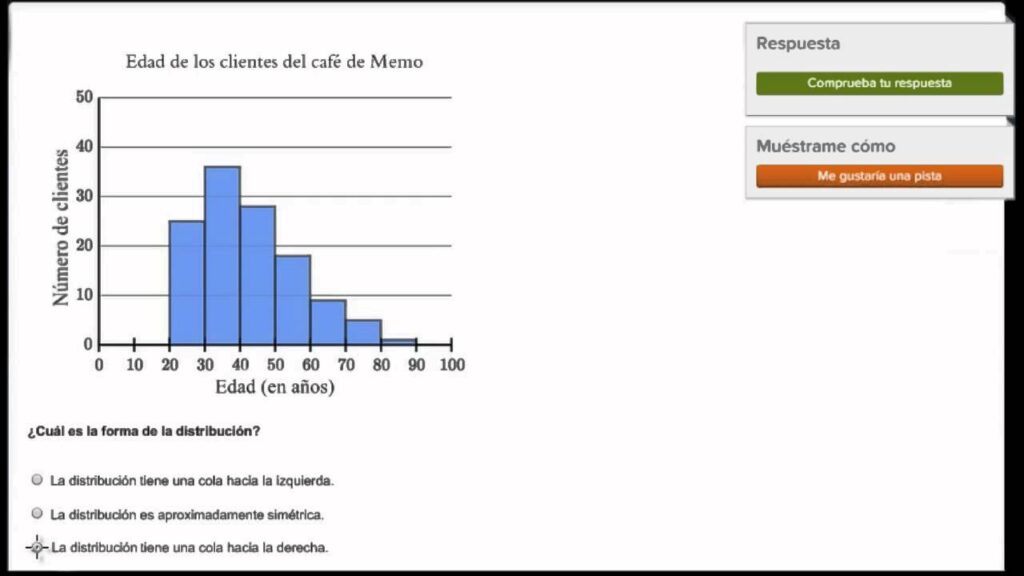
La campana de Gauss nos muestra cómo se distribuyen los datos alrededor de su media. Si la distribución es simétrica, es decir, tiene forma de campana, significa que los datos están equilibrados alrededor de la media y tienen una <dispersión similar tanto a la izquierda como a la derecha de esta. Por otro lado, si la distribución es asimétrica, esto indica que hay un sesgo hacia uno de los lados, lo que puede tener implicaciones en el análisis posterior de los datos.

2. Promedio y variabilidad

La campana de Gauss nos proporciona información sobre el promedio de los datos, representado por la media de la distribución. Además, también nos permite estimar la variabilidad de los datos mediante la desviación estándar. Si la campana es más estrecha y alta, esto indica que los datos tienen una baja variabilidad y se agrupan cerca de la media. En cambio, si la campana es más ancha y baja, esto implica una mayor variabilidad en los datos.

3. Probabilidades y intervalos

La campana de Gauss también se utiliza para calcular probabilidades y estimar intervalos de confianza. Al conocer la media y la desviación estándar, podemos determinar la probabilidad de que un valor esté dentro de un rango específico alrededor de la media. Esto es particularmente útil en estadística inferencial, donde las muestras se utilizan para hacer inferencias sobre una población más grande.

4. Detección de valores atípicos

Al analizar la distribución de datos utilizando la campana de Gauss, también podemos identificar posibles valores atípicos o datos erróneos que no siguen el patrón esperado. Estos valores extremos pueden afectar significativamente los cálculos posteriores y deben ser tratados con precaución.

La campana de Gauss nos proporciona valiosa información sobre la forma de una distribución de datos, su promedio, variabilidad, probabilidades y posibles valores atípicos. Nos permite comprender mejor cómo se distribuyen los datos y nos ayuda a tomar decisiones fundamentadas basadas en el análisis de estas distribuciones.

Cuáles son las limitaciones de la campana de Gauss en la modelización de fenómenos naturales o sociales

La campana de Gauss, también conocida como la distribución normal, es una función matemática que se utiliza ampliamente en diversas disciplinas para modelar la distribución de datos. Sin embargo, es importante tener en cuenta sus limitaciones cuando se aplica a fenómenos naturales o sociales.

Una de las principales limitaciones de la campana de Gauss es que asume que los datos siguen una distribución simétrica alrededor de su media. Esto significa que la cantidad de datos por encima y por debajo de la media debe ser igual. En la realidad, esto puede no ser cierto en muchos casos. Por ejemplo, en fenómenos socioeconómicos como la distribución de ingresos, a menudo nos encontramos con una gran concentración de datos en la parte inferior de la distribución y una cola larga hacia los ingresos más altos.

Otra limitación es que la campana de Gauss asume que los datos son independientes entre sí. Esto implica que el valor de un dato no afecta el valor de otro dato en la muestra. Sin embargo, en muchos fenómenos naturales o sociales, existe cierta dependencia entre los datos. Por ejemplo, en una red social, es probable que las interacciones entre individuos influyan en las decisiones y comportamientos de otros individuos, lo que puede llevar a una distribución de datos no independiente.

Además, la campana de Gauss también asume que la varianza de los datos es constante en toda la distribución. En algunos casos, sin embargo, la varianza puede no ser constante y puede cambiar según ciertas características de los datos o las condiciones del fenómeno estudiado. Por ejemplo, en la predicción del tráfico de una ciudad, es probable que la varianza de los tiempos de viaje varíe según la hora del día o el día de la semana.

Aunque la campana de Gauss es una herramienta poderosa para analizar y comprender la distribución de datos, tiene limitaciones significativas cuando se trata de modelar fenómenos naturales o sociales. Es importante ser conscientes de estas limitaciones y considerar otras distribuciones o técnicas estadísticas que sean más apropiadas para el caso específico que estamos estudiando.

Existen otras funciones o distribuciones matemáticas similares a la campana de Gauss

Además de la conocida campana de Gauss, existen otras funciones o distribuciones matemáticas que son similares en su forma y propiedades. A continuación, mencionaré algunas de estas funciones:

Distribución uniforme

La distribución uniforme es uno de los casos más simples en la teoría de probabilidad. Esta distribución se caracteriza por asignar una probabilidad constante a cada valor de un rango específico. En otras palabras, todos los valores dentro de ese rango tienen la misma probabilidad de ocurrir.

Distribución exponencial

La distribución exponencial es una función de densidad de probabilidad utilizada para describir el tiempo entre eventos independientes y constantes. Esta distribución se utiliza comúnmente en problemas relacionados con tiempos de espera, duraciones o tasas.

Distribución de Poisson

La distribución de Poisson es una distribución de probabilidad discreta que describe la probabilidad de ocurrencia de un número determinado de eventos en un intervalo de tiempo o espacio fijo. Esta distribución es ampliamente utilizada en situaciones donde se estudian eventos aleatorios y su frecuencia de aparición.

Distribución binomial

La distribución binomial es una función de probabilidad discreta que se utiliza para describir el número de éxitos en una secuencia de experimentos independientes y de dos posibles resultados: éxito o fracaso. Esta distribución es útil en problemas de conteo y en situaciones en las que se analizan características binarias.

Cabe destacar que aunque todas estas distribuciones tienen características distintas, comparten la propiedad de aproximar una campana de Gauss a medida que aumenta el tamaño de la muestra. Esta propiedad es conocida como el teorema del límite central y es fundamental en la estadística.

Cuál es la importancia de comprender la campana de Gauss en diferentes campos, como la economía, la psicología o la física

La campana de Gauss, también conocida como la distribución normal, es una función matemática que modela la forma en que los datos se distribuyen en un conjunto de observaciones. Su importancia radica en que esta distribución se encuentra presente en muchos fenómenos naturales y sociales, lo que nos permite comprender y predecir diversos patrones y comportamientos en diferentes campos del conocimiento.

Economía

En el campo de la economía, la campana de Gauss tiene una gran relevancia. Por ejemplo, en el análisis financiero, se utiliza para modelar la variabilidad en los rendimientos de inversiones y activos financieros. Al entender cómo se distribuyen estos rendimientos, se pueden tomar decisiones informadas sobre dónde invertir y qué tan arriesgada puede ser una inversión.

También es utilizada en el estudio de los ingresos económicos de la población. La distribución de los ingresos a nivel mundial sigue aproximadamente una distribución normal, con una concentración en la media y una disminución a medida que nos alejamos de ella. Esto permite estudiar la desigualdad económica y diseñar políticas públicas orientadas a su reducción.

Psicología

En psicología, la campana de Gauss se aplica para entender cómo se distribuyen diversos fenómenos. Por ejemplo, en pruebas psicométricas como los tests de inteligencia, se espera que el puntaje de la mayoría de las personas siga una distribución normal alrededor de una media determinada. Esto nos permite comparar el rendimiento de una persona con respecto a la población general.

Además, en la investigación psicológica, se utilizan los modelos de distribución normal para analizar y comprender fenómenos como la ansiedad, el estrés o los trastornos mentales. Estas distribuciones nos permiten entender la variabilidad en estos trastornos y diseñar intervenciones adecuadas basadas en las necesidades de cada individuo.

Física

En física, la campana de Gauss aparece en muchos fenómenos naturales. Por ejemplo, en la teoría cinética de los gases, describe cómo se distribuyen las velocidades de las moléculas dentro de un sistema gaseoso. Esta composición estándar nos permite comprender y predecir el comportamiento macroscópico del gas, como su presión, temperatura y volumen.

Además, la distribución normal también se utiliza en el campo de la mecánica cuántica. Por ejemplo, en el principio de incertidumbre de Heisenberg, se postula que la posición y momento de una partícula no se pueden conocer con certeza, sino que siguen una distribución de probabilidad, que es precisamente una distribución normal.

Preguntas frecuentes (FAQ)

1. ¿Qué es la campana de Gauss?

La campana de Gauss es una función matemática que describe una curva simétrica en forma de campana. Es utilizada para representar la distribución de datos en estadística y probabilidad.

2. ¿Cuál es la importancia de la campana de Gauss?

La campana de Gauss es importante porque permite comprender cómo se distribuyen los datos alrededor de su media. Nos ayuda a analizar la ocurrencia de eventos y pronosticar resultados.

3. ¿Cómo se calcula el área bajo la campana de Gauss?

El área bajo la campana de Gauss se puede calcular utilizando técnicas de integración en cálculo integral. Se utiliza para determinar la probabilidad de que un evento caiga dentro de un rango específico.

4. ¿Cuáles son las características principales de la campana de Gauss?

La campana de Gauss es simétrica y su pico está ubicado en el valor de la media. A medida que nos alejamos de la media, la curva va disminuyendo gradualmente, siguiendo una distribución normal.

5. ¿En qué situaciones se utiliza la campana de Gauss?

La campana de Gauss se utiliza en diversas áreas como investigación científica, análisis de datos, modelización estadística, evaluación de riesgos financieros y diseño de experimentos, entre otros.