Convierte rápidamente radianes a grados sexagesimales y domina las conversiones angulares en un abrir y cerrar de ojos

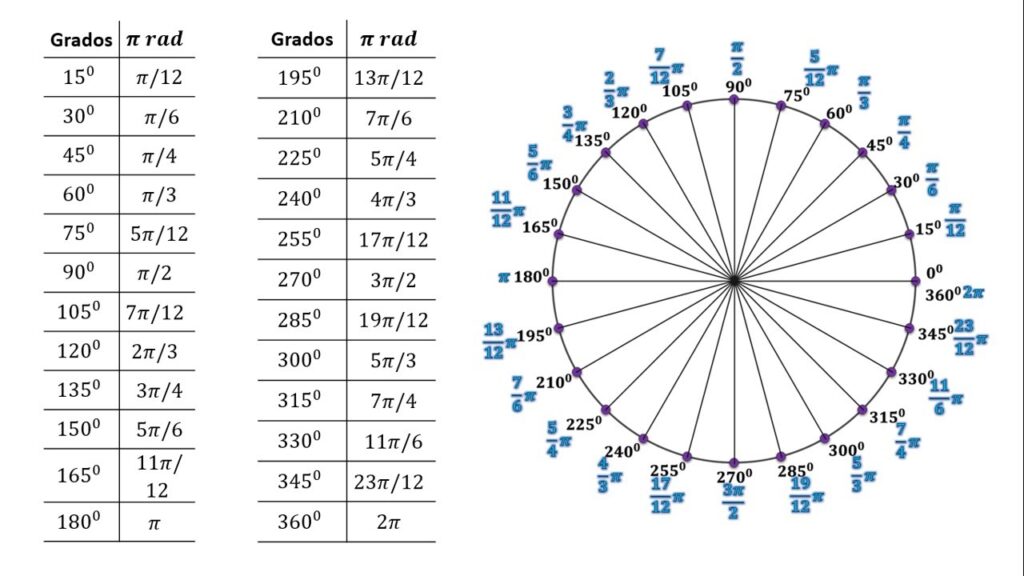
Las conversiones angulares son un aspecto importante en matemáticas y física, que nos permiten relacionar las mediciones realizadas en diferentes sistemas de unidades. En particular, la conversión de radianes a grados sexagesimales es una habilidad básica que todo estudiante de estas disciplinas debe dominar.

Te explicaremos de manera sencilla cómo convertir rápidamente medidas angulares expresadas en radianes a grados sexagesimales. Además, te daremos algunos ejemplos prácticos para que puedas practicar y afianzar tus conocimientos. No te pierdas esta oportunidad de mejorar tus habilidades en conversiones angulares.

Qué es un grado sexagesimal y cómo se relaciona con los ángulos

Un grado sexagesimal es una medida angular que se utiliza comúnmente en matemáticas y física. Se divide en 60 minutos, y cada minuto se divide en 60 segundos. Esta división en base 60 se deriva de la antigua práctica babilónica de contar y medir, que utilizaba un sistema numérico sexagesimal.

Los ángulos se pueden medir en grados sexagesimales utilizando el símbolo °. Por ejemplo, un ángulo recto mide 90°, un círculo completo mide 360° y así sucesivamente.

Para convertir entre radianes y grados sexagesimales, es necesario conocer la relación entre ellos. Un círculo completo equivale a 2π radianes, lo cual lleva a la fórmula de conversión:

grados = (radianes * 180) / π

De esta manera, si se te dan los radianes de un ángulo, puedes utilizar esta fórmula para convertirlo a grados sexagesimales.

Cuál es la fórmula para convertir radianes a grados sexagesimales

La fórmula para convertir radianes a grados sexagesimales es bastante sencilla. Se utiliza la siguiente ecuación:

grados = radianes * (180 / π)

En esta fórmula, "radianes" representa el valor en radianes que deseas convertir y "π" es una constante matemática que representa el número pi (~3.14159).

Para realizar la conversión, simplemente multiplicas el valor dado en radianes por el factor de conversión (180/π). El resultado será el equivalente en grados sexagesimales.

Por ejemplo, si tienes un ángulo de 2 radianes y quieres conocer su equivalente en grados sexagesimales, puedes utilizar la fórmula de la siguiente manera:

grados = 2 * (180 / π)

Realizando la operación obtendríamos:

grados = 2 * (57.2958)

Por lo tanto, el ángulo de 2 radianes equivale a aproximadamente 114.5916 grados sexagesimales.

Multiples conversiones de radianes a grados sexagesimales

A continuación, te mostraré algunos ejemplos adicionales de conversiones de radianes a grados sexagesimales para que puedas practicar:

• Radianes: 0.5
• Fórmula: grados = 0.5 * (180 / π)
• Resultado: 0.5 radianes equivalen a aproximadamente 28.6479 grados sexagesimales.

• Radianes: 1.2
• Fórmula: grados = 1.2 * (180 / π)
• Resultado: 1.2 radianes equivalen a aproximadamente 68.7549 grados sexagesimales.

• Radianes: 3.7
• Fórmula: grados = 3.7 * (180 / π)
• Resultado: 3.7 radianes equivalen a aproximadamente 212.1715 grados sexagesimales.

Recuerda que estos son solo ejemplos y que puedes realizar conversiones utilizando cualquier valor en radianes que desees.

Conclusión

Conocer la fórmula para convertir radianes a grados sexagesimales es esencial para poder trabajar con medidas angulares en diferentes sistemas de unidades. Siguiendo la ecuación adecuada, podrás realizar conversiones de manera rápida y precisa. Recuerda siempre utilizar el valor correcto de pi (~3.14159) en tu fórmula y practicar con diferentes ejemplos para mejorar tus habilidades en las conversiones angulares.

Cómo utilizar una calculadora científica para realizar conversiones angulares

Si estás buscando una forma rápida y sencilla de convertir radianes a grados sexagesimales, no busques más. Una calculadora científica puede ser tu mejor aliada en este proceso.

Cuando trabajamos con medidas angulares, es común encontrarnos con diferentes unidades, como radianes y grados sexagesimales. Mientras que los radianes son ampliamente utilizados en matemáticas y física, los grados sexagesimales son la unidad de medida angular más común en la vida cotidiana.

Afortunadamente, muchas calculadoras científicas modernas ofrecen la función de realizar conversiones angulares de manera automática. Si tienes acceso a una de estas calculadoras, puedes seguir los siguientes pasos para convertir rápidamente radianes a grados sexagesimales:

Paso 1: Accede al modo angular

En primer lugar, debes asegurarte de que tu calculadora esté configurada en el modo angular correcto. Busca la opción "MODE" o "MOD" en tu calculadora y selecciona el modo "DEG" para trabajar en grados sexagesimales.

Paso 2: Ingresa el valor en radianes

Ahora que tu calculadora está configurada correctamente, puedes ingresar el valor en radianes que deseas convertir. Puedes hacerlo utilizando las teclas numéricas de tu calculadora.

Paso 3: Utiliza la función de conversión

Una vez que hayas ingresado el valor en radianes, busca la función de conversión angular en tu calculadora. Puede estar etiquetada como "RAD->DEG" o algo similar. Presiona esa función y tu calculadora realizará automáticamente la conversión a grados sexagesimales.

En algunas calculadoras, es posible que debas presionar la tecla "SHIFT" o una tecla especial para acceder a las funciones trigonométricas y de conversión angular.

Paso 4: Obtén el resultado

Finalmente, tu calculadora te mostrará el resultado de la conversión en grados sexagesimales. Puedes utilizar este valor en tus cálculos o simplemente leerlo para entender mejor la medida angular.

Recuerda que esta función de conversión angular puede variar ligeramente según el modelo de tu calculadora científica. Es recomendable consultar el manual de usuario de tu calculadora para obtener instrucciones más detalladas sobre cómo realizar conversiones angulares específicas.

Con estos sencillos pasos, podrás convertir rápidamente radianes a grados sexagesimales utilizando una calculadora científica. No pierdas tiempo realizando cálculos manuales complicados, ¡deja que la tecnología haga el trabajo por ti!

Cuáles son algunos ejemplos prácticos de convertir radianes a grados sexagesimales

Conocer cómo convertir radianes a grados sexagesimales es de suma importancia en diversas áreas, como la física, la ingeniería y las matemáticas. A continuación, se presentan algunos ejemplos prácticos que ilustran la utilidad de esta conversión.

Ejemplo 1: Movimiento circular

Imaginemos que tenemos una partícula que se mueve en un círculo con una rapidez angular de 2 rad/s. Si queremos expresar esta velocidad angular en grados por segundo, debemos realizar la conversión correspondiente. Para ello, utilizamos la siguiente fórmula:

grados = radianes * (180/π)

Sustituyendo los valores conocidos:

• grados = 2 * (180/π)
• grados ≈ 114.59°

Por lo tanto, la velocidad angular en grados por segundo es aproximadamente 114.59°/s.

Ejemplo 2: Coordenadas polares

En coordenadas polares, un punto se define por su distancia al origen (r) y el ángulo que forma con el eje x positivo (θ). Supongamos que tenemos un punto con coordenadas polares (5, π/4). Si queremos expresar el ángulo en grados sexagesimales, debemos realizar la conversión correspondiente. Utilizando la fórmula mencionada anteriormente, tenemos:

grados = radianes * (180/π)

Sustituyendo los valores conocidos:

• grados = (π/4) * (180/π)
• grados ≈ 45°

Por lo tanto, el ángulo en grados sexagesimales es aproximadamente 45°.

Ejemplo 3: Fórmula de conversión entre radianes y grados

En algunos casos, es posible que necesitemos realizar la conversión en la otra dirección, es decir, de grados a radianes. En estos casos, podemos utilizar la siguiente fórmula:

radianes = grados * (π/180)

Esta fórmula nos permite convertir ángulos expresados en grados a su equivalente en radianes. Así, si tenemos un ángulo de 60° y deseamos obtener su valor en radianes:

radianes = 60 * (π/180)

Realizando la operación:

• radianes ≈ 1.05 rad

Por lo tanto, el ángulo de 60° equivale aproximadamente a 1.05 radianes.

Estos ejemplos demuestran cómo convertir rápidamente radianes a grados sexagesimales y viceversa en situaciones prácticas. Dominar esta habilidad es esencial para comprender y manipular correctamente las medidas angulares en diversas disciplinas. ¡En poco tiempo, podrás realizar estas conversiones en un abrir y cerrar de ojos!

Cuál es la importancia de dominar las conversiones angulares en diversas disciplinas

Las conversiones angulares son fundamentales en diversas disciplinas como matemáticas, física, trigonometría y navegación. Dominar estas conversiones es de suma importancia para los profesionales y estudiantes en estas áreas, ya que les permite comprender y resolver problemas que involucran mediciones y cálculos de ángulos en diferentes sistemas de medida.

En matemáticas, por ejemplo, las conversiones angulares son esenciales para trabajar con funciones trigonométricas y resolver ecuaciones que involucran ángulos. En física, estas conversiones son necesarias para comprender y calcular la cinemática y dinámica de objetos en movimiento, así como para analizar fuerzas y momentos de torsión.

En el campo de la trigonometría, las conversiones angulares son fundamentales para calcular razones trigonométricas en diferentes cuadrantes y resolver triángulos con medidas de ángulos en distintos sistemas. Además, en navegación, las conversiones angulares permiten determinar posiciones y rumbos en carta náutica, lo cual es esencial para la navegación marítima y aérea.

El dominio de las conversiones angulares también es relevante para aquellos que se dedican a la programación o diseño gráfico, ya que en ocasiones es necesario trabajar con coordenadas en términos de ángulos y necesitan convertir entre distintos sistemas para lograr los resultados deseados.

Dominar las conversiones angulares es esencial en diferentes disciplinas y campos profesionales. Esto permite a los especialistas realizar cálculos precisos, interpretar y analizar datos angulares de manera adecuada, así como desarrollar y aplicar modelos matemáticos y físicos con eficiencia. Por lo tanto, es crucial dedicar tiempo y esfuerzo para aprender y practicar estas conversiones para poder aprovechar al máximo las oportunidades y desafíos que se presenten en cada área de estudio o profesión.

Cuáles son algunas técnicas para agilizar el cálculo mental de conversiones angulares

Para agilizar el cálculo mental de conversiones angulares es importante conocer algunas técnicas que nos permitan realizar estas operaciones de manera rápida y precisa. A continuación, mencionaré algunas estrategias que te ayudarán a convertir rápidamente radianes a grados sexagesimales:

Técnica del factor de conversión

Una forma práctica de convertir radianes a grados sexagesimales es utilizar un factor de conversión adecuado. Para ello, recordemos que 2*π radianes equivalen a 360 grados. Por lo tanto, podemos establecer la siguiente relación:

1 radian = (180/π) grados

Así, para convertir cualquier valor en radianes a grados sexagesimales, simplemente multiplicamos dicho valor por el factor de conversión adecuado.

Ejemplo:

Supongamos que deseamos convertir 3 radianes a grados sexagesimales. Aplicando la técnica del factor de conversión, tendríamos lo siguiente:

3 radianes * (180/π) grados/radian = 171.88733853924697 grados

Por lo tanto, 3 radianes son aproximadamente 171.89 grados sexagesimales.

Técnica del uso de fracciones

Otra forma de simplificar la conversión de radianes a grados sexagesimales es mediante el uso de fracciones. Un angulo completo de 2 π radianes equivale a 360 grados, por lo que podemos establecer la siguiente igualdad:

2π radianes = 360 grados

A partir de esta igualdad, podemos utilizar una regla de tres para obtener el factor de conversión necesario:

1 radian = (360/2π) grados

Aplicando esta técnica, solo necesitamos simplificar la fracción en la ecuación anterior y multiplicar el valor dado en radianes por el resultado obtenido.

Ejemplo:

Consideremos ahora el caso en el que queremos convertir 4.5 radianes a grados sexagesimales. Aplicando la técnica de uso de fracciones, tendríamos lo siguiente:

4.5 radianes * (360/2π) grados/radianes = 257.87256396772346 grados

De esta manera, 4.5 radianes equivalen aproximadamente a 257.87 grados sexagesimales.

Estas técnicas son solo algunas de las muchas disponibles para agilizar el cálculo mental de conversiones angulares. Es importante practicar regularmente utilizando ejemplos reales para mejorar nuestra habilidad en estas operaciones y así dominar este aspecto fundamental de las matemáticas y la física.

Cómo verificar la precisión de la conversión de radianes a grados sexagesimales

La precisión de las conversiones es esencial al trabajar con ángulos en matemáticas y ciencias. En este artículo, aprenderás cómo verificar la precisión de la conversión de radianes a grados sexagesimales utilizando una fórmula simple.

Paso 1: Conoce la fórmula de conversión

La fórmula para convertir radianes a grados sexagesimales es la siguiente:

grados = (radianes * 180) / π

Donde π (pi) es el número irracional que representa la relación entre la circunferencia de un círculo y su diámetro, aproximadamente igual a 3.14159.

Paso 2: Selecciona un valor de prueba

Selecciona un valor de prueba en radianes que desees convertir a grados sexagesimales. Puedes elegir cualquier valor dentro del rango permitido para los radianes.

Paso 3: Calcula la conversión

Usando la fórmula mencionada anteriormente, calcula la conversión de radianes a grados sexagesimales para tu valor de prueba.

grados = (valor_radianes * 180) / π

Paso 4: Compara con una calculadora confiable

Utiliza una calculadora confiable o herramienta en línea para realizar la misma conversión y obtener el resultado correspondiente.

Paso 5: Verifica la precisión

Compara el resultado obtenido utilizando la fórmula con el resultado de la calculadora o herramienta en línea.

• Si ambos resultados son iguales o muy cercanos, tu conversión es precisa y puedes confiar en esta fórmula.
• Si hay una diferencia significativa entre los resultados, verifica si has ingresado correctamente el valor de prueba en la fórmula y repite los pasos anteriores. Si sigues obteniendo resultados incorrectos, es posible que haya un error en la fórmula utilizada.

Paso 6: Repite para diferentes valores de prueba

Para evaluar aún más la precisión de la conversión de radianes a grados sexagesimales, repite los pasos 2-5 para diferentes valores de prueba dentro del rango de radianes permitido. Al comparar los resultados obtenidos usando la fórmula y una calculadora confiable, podrás determinar si la fórmula proporciona resultados precisos en general.

Recuerda que la precisión en las conversiones angulares es crucial, especialmente al trabajar en aplicaciones científicas o técnicas donde se requiere un alto grado de exactitud. Siempre verifica la precisión de tus conversiones y utiliza fuentes confiables al realizar cálculos angulares.

Cuál es la relación entre radianes y grados iferentes sistemas de medición angular

Antes de sumergirnos en la conversión entre radianes y grados sexagesimales, es importante comprender la relación entre estos dos sistemas de medición angular.

Sistema de medida angular en grados

El sistema de medida angular más comúnmente utilizado es el sistema de grados sexagesimales. En este sistema, un círculo completo se divide en 360 partes iguales, llamadas grados. Cada grado, a su vez, se subdivide en 60 minutos, y cada minuto se subdivide en 60 segundos.

Así que, en resumen:

• 1 círculo = 360 grados
• 1 grado = 60 minutos
• 1 minuto = 60 segundos

Sistema de medida angular en radianes

Los radianes son una unidad de medida angular utilizada principalmente en el campo de las matemáticas y la física. A diferencia de los grados, los radianes se basan en la longitud del radio del círculo.

En un círculo completo, hay 2π (pi) radianes. Pi es una constante matemática que representa la relación entre la circunferencia de un círculo y su diámetro.

Entonces, podemos establecer la siguiente relación:

2π radianes = 360 grados

Esta es una equivalencia importante para recordar cuando queremos convertir entre radianes y grados.

Conversión de radianes a grados sexagesimales

Para convertir una medida en radianes a grados sexagesimales, simplemente usamos la relación anterior:

Medida en grados = (Medida en radianes * 180) / π

Por ejemplo, si tenemos una medida angular de 1.5 radianes y queremos conocer su equivalente en grados sexagesimales, simplemente hacemos lo siguiente:

Medida en grados = (1.5 radianes * 180) / π ≈ 85.94 grados

Así que 1.5 radianes serían aproximadamente igual a 85.94 grados sexagesimales.

Entender la relación entre radianes y grados sexagesimales es fundamental para dominar las conversiones angulares. Con la fórmula proporcionada, puedes convertir fácilmente entre ambos sistemas de medición y realizar cálculos precisos en tus problemas matemáticos o físicos.

1. ¿Cómo se realiza la conversión de radianes a grados sexagesimales?

Para convertir radianes a grados sexagesimales, multiplica el valor en radianes por 180 y divide entre π.

2. ¿Cuál es la fórmula para convertir grados sexagesimales a radianes?

La fórmula para convertir grados sexagesimales a radianes es multiplicar el valor en grados por π y dividir entre 180.

3. ¿Cuál es el valor de π en las conversiones angulares?

El valor de π en las conversiones angulares es aproximadamente 3.14159.

4. ¿Cómo se convierten minutos y segundos a grados en la conversión sexagesimal?

Para convertir minutos o segundos a grados en la conversión sexagesimal, divide el valor por 60 (para los minutos) o por 3600 (para los segundos).

5. ¿Existe algún truco o fórmula para realizar rápidamente las conversiones angulares?

No existe un truco específico, pero practicar y familiarizarse con las fórmulas de conversión ayudará a realizar las conversiones más rápidamente.