Conviértete en un experto en matemáticas: Aprende cómo sacar el área con fracciones y domina los cálculos de forma fácil y rápida

Las matemáticas son una disciplina fundamental en la educación, y el cálculo del área es uno de los conceptos más importantes dentro de esta materia. El área se refiere a la medida de superficie de una figura geométrica y puede calcularse utilizando diferentes fórmulas dependiendo del tipo de figura. Sin embargo, cuando las dimensiones de una figura se expresan en forma de fracciones, algunos estudiantes pueden enfrentar dificultades al realizar los cálculos.

Exploraremos cómo calcular el área de figuras geométricas utilizando fracciones. Veremos ejemplos detallados paso a paso que te permitirán comprender el proceso de manera clara y concisa. Además, proporcionaremos algunas estrategias y consejos prácticos para simplificar los cálculos y garantizar un aprendizaje efectivo. Al final, podrás aplicar estos conocimientos para resolver problemas de área con facilidad y dominar este aspecto de las matemáticas.

Cómo calcular el área de figuras geométricas usando fracciones

Calcular el área de figuras geométricas puede ser un desafío para muchos estudiantes. Sin embargo, con el uso adecuado de fracciones, este proceso puede volverse mucho más sencillo y comprensible.

Para calcular el área de una figura geométrica utilizando fracciones, es importante conocer la fórmula correcta para cada tipo de figura. A continuación, repasaremos las fórmulas y los pasos necesarios para calcular el área de algunos de los polígonos más comunes:

Triángulo

El área de un triángulo se calcula multiplicando la base por la altura y dividiendo el resultado por 2:

Área del triángulo = (base * altura) / 2

Si ambos valores (base y altura) están expresados como fracciones, simplemente debes aplicar la regla básica de las fracciones: multiplicar numerador por numerador y denominador por denominador.

Rectángulo

El área de un rectángulo se calcula multiplicando la base por la altura:

Área del rectángulo = base * altura

Nuevamente, si la base y la altura están expresadas como fracciones, solo debes llevar a cabo la multiplicación de manera apropiada utilizando las reglas de las fracciones.

Cuadrado

El área de un cuadrado se calcula elevando al cuadrado uno de los lados:

Área del cuadrado = lado * lado

Si el lado del cuadrado está representado por una fracción, simplemente debes multiplicar el numerador por sí mismo y el denominador por sí mismo también.

Círculo

El área de un círculo se calcula multiplicando el cuadrado del radio por π (pi):

Área del círculo = radio * radio * π

En este caso, si el radio está expresado como una fracción, deberás realizar las operaciones indicadas y luego multiplicar el resultado obtenido por π.

Recuerda que, en todos los casos, es importante simplificar la fracción resultante si es posible. Esto facilitará la lectura y comparación de diferentes áreas.

Ahora que conoces las fórmulas para calcular el área de estas figuras geométricas utilizando fracciones, práctica aplicándolas con diferentes ejemplos. Verás cómo, con el tiempo, te familiarizarás más con estos cálculos y podrás resolverlos de forma fácil y rápida.

Cuáles son las reglas básicas para sacar el área con fracciones

Para sacar el área con fracciones, es necesario recordar algunas reglas básicas que te serán de gran ayuda. A continuación, se presentan las reglas más importantes a tener en cuenta:

Regla 1: Convierte la fracción en un número decimal

Antes de comenzar a calcular el área, es conveniente convertir las fracciones en números decimales. Esto facilitará los cálculos y permitirá obtener resultados más precisos.

Por ejemplo, si tienes una fracción como 3/4, puedes dividir 3 entre 4 y obtener 0.75. De esta manera, podrás trabajar con decimales en lugar de fracciones más complicadas.

Regla 2: Multiplica la base por la altura

La fórmula general para calcular el área de una figura es multiplicar la base por la altura. En el caso de las fracciones, debes asegurarte de multiplicar tanto la parte entera como el numerador y denominador de la fracción.

Por ejemplo, si tienes un rectángulo con una base de 2 3/4 y altura de 1 1/2, debes multiplicar 2 por 3/4 y luego multiplicar 1 por 1/2. Luego, suma ambos resultados para obtener el área total.

Regla 3: Simplifica el resultado, si es posible

Después de hacer los cálculos, es recomendable simplificar el resultado obtenido si es posible. Para simplificar una fracción, debes buscar un divisor común entre el numerador y denominador y dividir ambos números por ese divisor.

Por ejemplo, si el resultado del cálculo es 5/8, puedes simplificarlo dividiendo tanto el numerador como el denominador por 1. Esto dará como resultado la fracción 5/8 en su forma más sencilla.

• Ejemplo 1:

Tienes un triángulo con una base de 3/4 y altura de 2/5. Para calcular el área, multiplica 3/4 por 2/5:
(3/4) * (2/5) = 6/20

Luego, simplifica el resultado: 6/20 se puede dividir por 2.
(6/20) / 2 = 3/10

• Ejemplo 2:

Tienes un círculo con un radio de 5/8. Para calcular el área, usa la fórmula del área de un círculo: A = πr².
Reemplaza el valor del radio por 5/8:
A = π(5/8)²

Eleva al cuadrado el número decimal equivalente al radio para obtener la respuesta precisa.

Recuerda que practicar constantemente te ayudará a familiarizarte más con las reglas y a mejorar tus habilidades para sacar el área con fracciones. ¡No dudes en practicar con diferentes ejercicios y situaciones para dominar este tema!

Qué fórmulas se utilizan para calcular el área de triángulos, cuadrados y círculos con fracciones

Calcular el área de figuras geométricas es un concepto fundamental en matemáticas. A través del uso de fórmulas específicas, podemos determinar de manera precisa la cantidad de espacio que ocupa una figura en un plano.

En el caso de las figuras con fracciones, como los triángulos, cuadrados y círculos, existen fórmulas particulares que nos permiten calcular su área de forma rápida y sencilla. A continuación, te explicaremos cada una de estas fórmulas:

Cálculo del área de un triángulo con fracciones

Para calcular el área de un triángulo, se utiliza la fórmula:

Área = base * altura / 2

La base representa la longitud de uno de los lados del triángulo y la altura es la distancia perpendicular desde la base al vértice opuesto. Para calcular el área usando fracciones, simplemente realizamos la multiplicación de la base por la altura y luego dividimos el resultado entre 2.

Cálculo del área de un cuadrado con fracciones

El área de un cuadrado se puede calcular utilizando la siguiente fórmula:

Área = lado * lado

Donde el lado representa la longitud de cualquiera de los cuatro lados del cuadrado. Para calcular el área con fracciones, multiplicamos el valor del lado por sí mismo.

Cálculo del área de un círculo con fracciones

El área de un círculo se calcula utilizando la siguiente fórmula:

Área = π * radio^2

Donde π (pi) es una constante aproximada a 3.1416 y el radio es la distancia desde el centro del círculo hasta cualquier punto de su circunferencia. Para calcular el área con fracciones, simplemente elevamos al cuadrado el valor del radio y luego multiplicamos por π.

Con estas fórmulas, calcular el área de triángulos, cuadrados y círculos con fracciones se vuelve más sencillo y rápido. Recuerda siempre utilizar el valor adecuado de cada medida y simplificar las fracciones si es necesario para obtener resultados precisos.

Cómo simplificar las fracciones al sacar el área de una figura geométrica

Al calcular el área de una figura geométrica con fracciones, es importante simplificar las fracciones involucradas para obtener un resultado más preciso y fácil de manejar. Simplificar una fracción implica dividir tanto el numerador como el denominador por su máximo común divisor (MCD).

Para explicar este proceso, consideremos un ejemplo práctico. Supongamos que deseamos calcular el área de un triángulo cuya base mide 3/4 de metro y cuya altura es de 2/3 de metro.

Lo primero que debemos hacer es simplificar ambas fracciones. Para ello, tenemos que encontrar el MCD de 3 y 4, así como el MCD de 2 y 3.

El MCD de 3 y 4 es 1, ya que no tienen divisores comunes más allá del 1. Por otro lado, el MCD de 2 y 3 también es 1, ya que ambos números son primos entre sí.

Una vez encontrados los MCD, procedemos a simplificar cada fracción. Dividimos el numerador y el denominador de la fracción por su respectivo MCD.

Para la fracción 3/4, obtenemos:


3 ÷ 1 = 3
4 ÷ 1 = 4


Por lo tanto, la fracción simplificada es 3/4.

Para la fracción 2/3, obtenemos:


2 ÷ 1 = 2
3 ÷ 1 = 3


Por lo tanto, la fracción simplificada es 2/3.

Una vez que tenemos las fracciones simplificadas, procedemos a calcular el área utilizando la fórmula A = (base * altura) / 2. Reemplazamos las fracciones simplificadas en la fórmula:


A = (3/4 * 2/3) / 2


Multiplicamos los numeradores y los denominadores respectivamente:


A = (6/12) / 2


Simplificamos la fracción resultante:


A = 1/4


Por lo tanto, el área del triángulo es de 1/4 de metro cuadrado.

Este proceso nos permite obtener resultados más precisos al trabajar con fracciones, ya que simplificarlas reduce cualquier posible error o confusión en los cálculos. Además, los resultados simplificados son más fáciles de interpretar y manipular en futuras operaciones matemáticas.

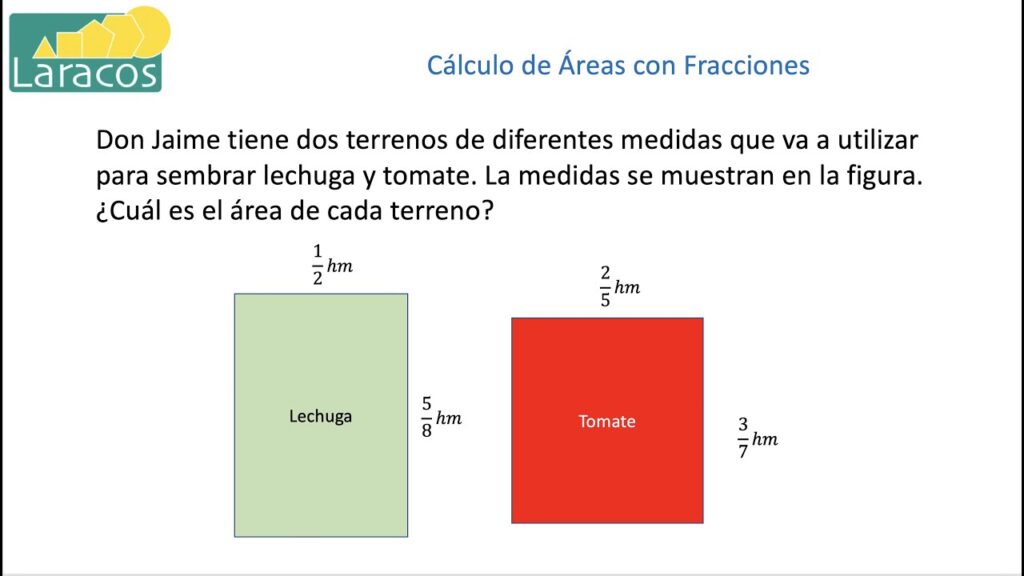
Cuáles son los pasos para calcular el área de un rectángulo con fracciones

Si deseas simplificar las fracciones antes de realizar el cálculo, puedes seguir estos pasos adicionales:

• Paso 1: Factoriza tanto el numerador como el denominador.
• Paso 2: Cancela los factores comunes entre el numerador y el denominador.
• Paso 3: Realiza la multiplicación de los nuevos valores simplificados para obtener el área del rectángulo.

Por ejemplo, si tienes un rectángulo con una base de ⅓ y una altura de ⅔, puedes simplificar las fracciones de la siguiente manera:

• Para la base: ⅓ = 1 / 3. Factoreamos 1 en números primos: 1 = 1 x 1. Luego, cancelamos el factor común (1) entre el numerador y el denominador.
• Para la altura: ⅔ = 1 / 2. Factoreamos 1 en números primos: 1 = 1 x 1. Luego, cancelamos el factor común (1) entre el numerador y el denominador.

Ahora, multiplicamos las fracciones simplificadas: 1/3 x 1/2 = 1/6. Por lo tanto, el área del rectángulo es de 1/6 unidades cuadradas.

Recuerda que estos pasos adicionales son opcionales y pueden ser útiles cuando deseas trabajar con fracciones simplificadas en tus cálculos.

Cómo calcular el área de un triángulo utilizando fracciones

Calcular el área de un triángulo utilizando fracciones puede parecer complicado al principio, pero en realidad es bastante sencillo una vez que comprendes el proceso. Aquí te explicaré paso a paso cómo hacerlo:

Paso 1: Conoce la fórmula

La fórmula para calcular el área de un triángulo es A = 1/2 * base * altura, donde A representa el área, base es la longitud de uno de los lados del triángulo y altura es la distancia perpendicular desde la base hasta el vértice opuesto.

Paso 2: Identifica la base y la altura

Para utilizar la fórmula correctamente, debes identificar la base y la altura del triángulo. La base es uno de los lados del triángulo y la altura es la distancia perpendicular desde la base hasta el vértice opuesto. Asegúrate de tener estos valores antes de continuar con el cálculo.

Paso 3: Sustituye los valores en la fórmula

Una vez que tengas la base y la altura, sustituye esos valores en la fórmula del área del triángulo. Recuerda multiplicar la base por la altura y luego dividir el resultado entre 2.

A = 1/2 * base * altura

Paso 4: Simplifica la fracción si es necesario

Si obtuviste una fracción como resultado en el paso anterior, puedes simplificarla si es necesario. Esto implica buscar un número que divida tanto al numerador como al denominador de la fracción sin dejar residuo. Por ejemplo, si obtuviste 3/6 como resultado, puedes simplificarlo dividiendo ambos términos por 3 para obtener 1/2.

Paso 5: Calcula el área del triángulo

Finalmente, realiza las operaciones necesarias para obtener el valor exacto o aproximado del área del triángulo en función de la base y la altura que proporcionaste inicialmente. ¡Y eso es todo! Has calculado el área de un triángulo utilizando fracciones.

Ahora que conoces el proceso para calcular el área de un triángulo utilizando fracciones, podrás resolver problemas matemáticos donde esta habilidad sea necesaria. Recuerda practicar regularmente para mejorar tus habilidades en matemáticas y convertirte en un experto en el cálculo de áreas de formas geométricas.

Cuál es la forma más rápida de calcular el área de un círculo con fracciones

Calcular el área de un círculo puede ser un poco complicado si no se conocen las fórmulas adecuadas. Sin embargo, con el uso de fracciones, es posible realizar este cálculo de forma rápida y sencilla.

La fórmula para calcular el área de un círculo es:

A = π * r^2

Donde "A" representa el área del círculo, "π" es una constante que representa la relación entre la circunferencia y el diámetro de cualquier círculo, y "r" es el radio del círculo.

Al utilizar fracciones en lugar de decimales para el valor de π, podemos obtener resultados más precisos y evitar redondear demasiado.

Por ejemplo, si queremos calcular el área de un círculo con un radio de 3 unidades utilizando fracciones, podemos hacer lo siguiente:

1. Determinar el valor exacto de π. En este caso, utilizaremos π como una fracción: π = 22/7.
2. Elevar al cuadrado el valor del radio: r^2 = 3^2 = 9.
3. Multiplicar el resultado del paso anterior por el valor de π en fracción: A = (22/7) * 9 = 198/7.

Por lo tanto, el área del círculo será de 198/7 unidades.

Es importante tener en cuenta que al utilizar fracciones, los cálculos pueden ser más tediosos y requerir una mayor precisión en las operaciones. Sin embargo, el resultado final será más exacto y evitará redondeos innecesarios.

Qué estrategias o trucos puedo utilizar para agilizar los cálculos de áreas con fracciones

Calcular el área de figuras con fracciones puede parecer complicado al principio, pero existen estrategias y trucos que te pueden ayudar a agilizar estos cálculos. A continuación, te presentamos algunos de ellos:

1. Utiliza la fórmula general para calcular áreas

Cuando te enfrentes a una figura con fracciones, como un triángulo o un cuadrado, utiliza la fórmula general para calcular su área. Por ejemplo, en el caso de un triángulo, puedes utilizar la fórmula A = (b * h) / 2, donde b es la base del triángulo y h es la altura.

2. Simplifica las fracciones antes de hacer los cálculos

Siempre que sea posible, simplifica las fracciones antes de realizar los cálculos. Esto te permitirá trabajar con números más pequeños y facilitará tus operaciones matemáticas. Por ejemplo, si encuentras una fracción como 4/8, puedes simplificarla dividiendo ambos números por su máximo común divisor, en este caso 4. La fracción simplificada sería 1/2.

3. Utiliza el método de descomposición

En algunas ocasiones, puede ser beneficioso descomponer una figura con fracciones en varias figuras más simples. Por ejemplo, si tienes un trapecio con fracciones en su base y altura, puedes descomponerlo en un rectángulo y dos triángulos. Luego, calcula el área de cada una de estas figuras por separado y suma los resultados para obtener el área total del trapecio.

4. Practica con ejercicios y problemas

La mejor manera de dominar los cálculos de áreas con fracciones es practicar con una amplia variedad de ejercicios y problemas. Esto te ayudará a familiarizarte con las distintas estrategias y te permitirá desarrollar tu destreza en este tipo de cálculos. Busca ejercicios en libros de texto, en línea o crea tus propios problemas para resolverlos.

5. Utiliza recursos tecnológicos

Aprovecha las herramientas tecnológicas disponibles para facilitar tus cálculos. Existen calculadoras que pueden trabajar con fracciones y te pueden mostrar paso a paso cómo realizar los cálculos. También puedes utilizar programas de dibujo o geometría en línea para visualizar las figuras con fracciones antes de calcular sus áreas.

No olvides practicar regularmente y tener paciencia. Con el tiempo, te sentirás más cómodo y seguro al calcular áreas con fracciones, convirtiéndote en un experto en matemáticas.

Cómo aplicar el teorema de Pitágoras al calcular áreas con fracciones en triángulos rectángulos

El teorema de Pitágoras es una herramienta fundamental en matemáticas que nos permite calcular las áreas de triángulos rectángulos de forma precisa. Sin embargo, cuando las dimensiones involucradas son fracciones, el cálculo puede resultar un poco más complicado. A continuación, te mostramos cómo aplicar el teorema de Pitágoras al calcular áreas con fracciones en triángulos rectángulos de manera sencilla y rápida.

Paso 1: Identifica las longitudes de los catetos

• Para comenzar, necesitas identificar las longitudes de los dos catetos del triángulo rectángulo. Estos catetos se encuentran en los lados que forman el ángulo recto.
• Supongamos que uno de los catetos mide "a" y el otro cateto mide "b". Ambas medidas se expresan como fracciones.

Paso 2: Aplica el teorema de Pitágoras

• Una vez que tienes las longitudes de los catetos identificadas, puedes aplicar el teorema de Pitágoras, el cual establece que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
• Eleva al cuadrado las longitudes de los catetos: a² y b².
• Suma ambos resultados: a² + b².

Paso 3: Calcula la hipotenusa

• Una vez que tienes la suma de los cuadrados de los catetos, necesitas calcular la raíz cuadrada de ese valor para obtener la longitud de la hipotenusa.
• Este paso es fundamental, ya que la hipotenusa representa el lado más largo del triángulo rectángulo y será la base para calcular el área utilizando fracciones.

Paso 4: Calcula el área aplicando las propiedades de las fracciones

• Una vez que hayas determinado la longitud de la hipotenusa y sabiendo que estamos trabajando con fracciones, debes aplicar las propiedades algebraicas de las fracciones para simplificar la expresión y obtener una fracción reducida.
• Para calcular el área, utiliza la fórmula Área = (base * altura) / 2.
• La base será igual a la longitud de uno de los catetos, mientras que la altura será igual a la longitud del otro cateto.
• Multiplica ambas longitudes y reduce la fracción resultante si es necesario.

Siguiendo estos pasos con cuidado, podrás sacar fácilmente el área de un triángulo rectángulo con fracciones utilizando el teorema de Pitágoras. Recuerda practicar con diferentes ejemplos para consolidar tus habilidades y convertirte en un experto en cálculos matemáticos.

Dónde puedo encontrar ejercicios y problemas para practicar el cálculo de áreas con fracciones

Para practicar el cálculo de áreas con fracciones, hay varias opciones disponibles en línea. Aquí te presentamos algunas plataformas y recursos donde puedes encontrar ejercicios y problemas para practicar y mejorar tus habilidades en este tema.

1. Páginas web educativas

Hay una gran cantidad de páginas web educativas que ofrecen ejercicios interactivos y problemas relacionados con el cálculo de áreas usando fracciones. Algunas de estas páginas incluyen:

• Math is Fun: Esta página ofrece explicaciones claras y ejemplos paso a paso, así como ejercicios y juegos interactivos para reforzar el aprendizaje de las áreas con fracciones.
• Khan Academy: Khan Academy es una plataforma educativa que ofrece lecciones en video y ejercicios prácticos en una amplia variedad de temas matemáticos, incluyendo el cálculo de áreas con fracciones.
• IXL: IXL es una plataforma de aprendizaje en línea que incluye ejercicios estructurados y secuenciados para practicar habilidades matemáticas, incluyendo el cálculo de áreas con fracciones.

2. Libros de texto y guías de estudio

Otra opción para encontrar ejercicios y problemas sobre el cálculo de áreas con fracciones es consultar libros de texto y guías de estudio de matemáticas. Muchos libros de matemáticas incluyen secciones específicas dedicadas al cálculo de áreas con fracciones, con ejemplos resueltos y problemas para practicar.

3. Plataformas de aprendizaje en línea

Existen plataformas de aprendizaje en línea que ofrecen cursos especializados en matemáticas, donde puedes acceder a ejercicios, problemas y evaluaciones relacionados con el cálculo de áreas usando fracciones. Algunas de estas plataformas incluyen Coursera, Udemy y edX.

4. Recursos y tutoriales en YouTube

YouTube también es una fuente de recursos educativos donde puedes encontrar tutoriales y videos explicativos sobre cómo calcular áreas con fracciones. Busca canales educativos que se especialicen en matemáticas y revisa su contenido relacionado con este tema.

Recuerda que la práctica constante es clave para mejorar tus habilidades en el cálculo de áreas con fracciones. No te limites a ejercicios básicos, desafíate con problemas más complejos y busca diferentes tipos de ejercicios que te ayuden a dominar este tema de manera integral.

El área es la cantidad de espacio dentro de una figura o superficie.

Una fracción representa una parte de una unidad o un todo dividido en partes iguales.

Para calcular el área con fracciones, debes multiplicar el largo por el ancho y expresarlo como una fracción simplificada.

La fórmula para calcular el área de un rectángulo con fracciones es: área = largo x ancho.

Para simplificar una fracción, divide el numerador y el denominador por su máximo común divisor.