¡Descubre cómo calcular fácilmente el área de un trapecio! Los secretos que necesitas conocer sobre la fórmula de área de trapecio. Aprende a calcular el área de un trapecio en simples pasos. Domina las matemáticas con esta guía completa de cómo determinar el área de un trapecio

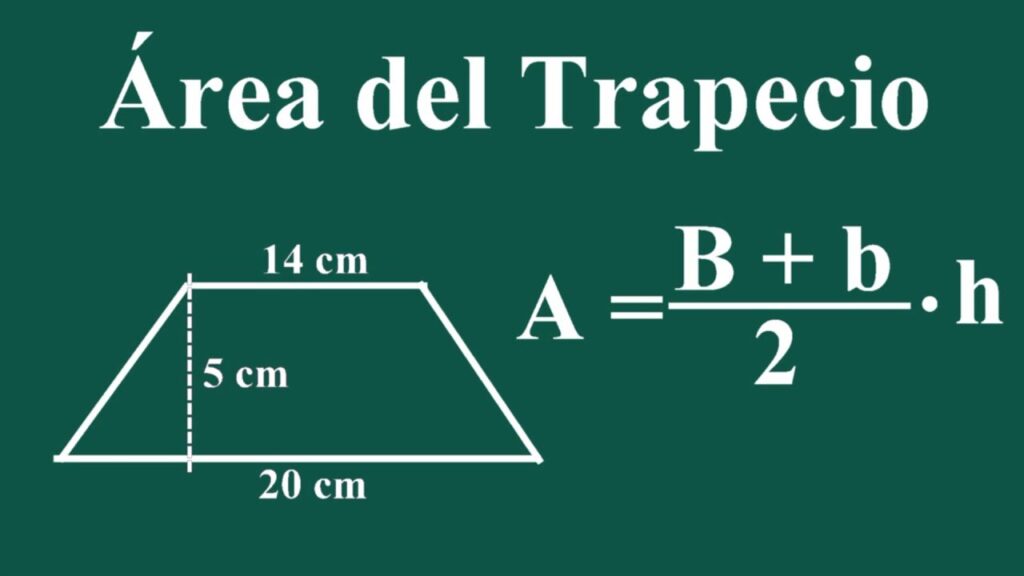
El cálculo del área es una habilidad fundamental en matemáticas y geometría. Entre las diversas figuras geométricas, el trapecio es una de las más comunes y puede resultar complicado determinar su área si no se conocen los métodos adecuados.

En este artículo aprenderemos cómo calcular el área de un trapecio usando fórmulas sencillas y paso a paso. Comenzaremos explicando qué es un trapecio y las propiedades que lo caracterizan, para luego adentrarnos en la fórmula del área de un trapecio y cómo aplicarla correctamente. Además, compartiremos algunos ejemplos prácticos y consejos útiles para facilitar el proceso de cálculo. ¡No te pierdas esta guía completa sobre cómo determinar el área de un trapecio!

Cuál es la fórmula para calcular el área de un trapecio

El área de un trapecio se puede calcular utilizando una fórmula específica. Esta fórmula se basa en la **altura del trapecio** y las **longitudes de sus bases**. A continuación, te mostraré cómo funciona:

Fórmula del área de un trapecio

La fórmula para calcular el **área de un trapecio** es la siguiente:

Área = (base mayor + base menor) * altura / 2

En esta fórmula, "**base mayor**" se refiere a la longitud de la base más larga del trapecio, "**base menor**" se refiere a la longitud de la base más corta del trapecio, y "**altura**" se refiere a la distancia perpendicular entre las dos bases.

Es importante recordar que todas las longitudes utilizadas en la fórmula deben estar en la misma **unidad de medida**, ya sea centímetros, metros o cualquier otra unidad.

Ejemplo práctico

Para comprender mejor cómo se utiliza esta fórmula, veamos un ejemplo práctico. Supongamos que tenemos un trapecio con una base mayor de 8 centímetros, una base menor de 6 centímetros y una altura de 4 centímetros.

Aplicando la fórmula, podemos calcular el área de la siguiente manera:

Área = (8 + 6) * 4 / 2

Simplificando la expresión, obtenemos:

Área = 14 * 4 / 2

Finalmente, realizamos la multiplicación y división para obtener el resultado:

Área = 56 / 2

Área = 28 cm²

Por lo tanto, el área del trapecio en este ejemplo es de **28 centímetros cuadrados**.

Recuerda que la fórmula del área de un trapecio solo se aplica a trapecios específicos. Si tienes otro tipo de figura geométrica, se requeriría una fórmula diferente para calcular su área.

Con esta fórmula y el ejemplo práctico, ahora puedes calcular fácilmente el área de cualquier trapecio que encuentres.

Cómo se pueden identificar las medidas necesarias en un trapecio para calcular su área

Para calcular el área de un trapecio, es fundamental tener en cuenta las medidas necesarias. Estas medidas incluyen la longitud de sus bases y la altura del trapecio.

La base mayor (B) del trapecio es la parte inferior, mientras que la base menor (b) es la parte superior. Es importante tener en cuenta que las bases deben ser paralelas entre sí. Además, la altura del trapecio (h) es la distancia perpendicular entre las bases.

Una vez que se tienen estas tres medidas, se puede aplicar la fórmula correspondiente para calcular el área del trapecio.

Fórmula del área de un trapecio

La fórmula para calcular el área de un trapecio es:

Área = (B + b) * h / 2

Esta fórmula utiliza la suma de las bases multiplicada por la altura, y luego se divide el resultado entre 2.

Ejemplo de cálculo de área de un trapecio

Supongamos que tenemos un trapecio con una base mayor de 10 cm, una base menor de 6 cm y una altura de 8 cm. Para calcular el área, podemos utilizar la fórmula mencionada anteriormente:

Área = (10 + 6) * 8 / 2 = 64 cm²

En este ejemplo, el área del trapecio es de 64 cm².

Cómo resolver problemas de áreas de trapecios

Al resolver problemas que involucren áreas de trapecios, es importante identificar las medidas proporcionadas y determinar cuáles se requieren para aplicar la fórmula de área del trapecio.

En algunos casos, se pueden proporcionar la base mayor y menor, pero no la altura. En estos casos, es posible que sea necesario utilizar técnicas de geometría o trigonometría para encontrar el valor de la altura antes de realizar el cálculo del área.

Además, es fundamental recordar que todas las medidas deben estar en la misma unidad antes de aplicar la fórmula. Si es necesario, se deben convertir las medidas a la misma unidad antes de proceder con el cálculo.

Calcular el área de un trapecio puede ser fácil siempre y cuando se tengan en cuenta las medidas necesarias y se aplique la fórmula adecuada. Recordar los conceptos básicos de las bases y la altura del trapecio permitirá resolver problemas relacionados con el área de una manera eficiente.

Cuál es la diferencia entre una base mayor y una base menor en un trapecio

En la geometría del trapecio, el concepto de las bases es fundamental para calcular su área. Un trapecio es un cuadrilátero que tiene dos lados paralelos llamados bases. Cada base tiene una longitud y una posición dentro del trapecio.

La diferencia entre la base mayor y la base menor radica en su tamaño relativo. La base mayor es el lado más largo del trapecio, mientras que la base menor es el lado más corto. Ambas bases son líneas paralelas entre sí, pero tienen diferentes longitudes.

Es importante recordar que la base mayor siempre está opuesta al ángulo agudo del trapecio, mientras que la base menor está opuesta al ángulo obtuso. Esta distinción es crucial cuando se utiliza la fórmula de área del trapecio.

Cálculo del área del trapecio

Para calcular el área de un trapecio, se utiliza la fórmula:
Área = (Base Mayor + Base Menor) * Altura / 2

Donde la altura es la distancia perpendicular entre las bases del trapecio. Para obtener resultados precisos, generalmente se requiere medir la altura en línea recta desde la base mayor a la base menor. Si no tienes información sobre la altura, existen diferentes métodos para calcularla utilizando otros datos disponibles.

• Si conoces los lados laterales y los ángulos del triángulo formado por la altura y las bases, puedes utilizar trigonometría para calcular la altura.
• Si conoces los lados del trapecio y los ángulos, puedes utilizar el teorema de Pitágoras para hallar la altura.
• Si conoces las longitudes de los lados del trapecio y la distancia entre las bases (no necesariamente perpendicular), puedes utilizar el teorema de Herón para calcular el área.

Recuerda que el cálculo del área del trapecio solo es válido si ambas bases son líneas paralelas. De lo contrario, se consideraría otro polígono.

Ejemplo práctico de cálculo de área del trapecio

Supongamos que tenemos un trapecio con una base mayor de longitud 8 cm, una base menor de longitud 4 cm y una altura de 5 cm.

Para calcular el área utilizando la fórmula del trapecio, simplemente sustituimos los valores en la ecuación:

Área = (8 + 4) * 5 / 2

Área = 12 * 5 / 2

Área = 60 / 2

Área = 30 cm^2

Por lo tanto, el área del trapecio es de 30 cm^2.

Como puedes ver, calcular el área de un trapecio no es complicado siempre y cuando tengas las medidas adecuadas y utilices la fórmula correcta. Ahora que conoces los conceptos básicos, podrás resolver problemas de áreas de trapecios con facilidad.

Cuáles son los pasos para calcular el área de un trapecio

Calcular el área de un trapecio puede parecer complicado al principio, pero en realidad es bastante sencillo si sigues los pasos adecuados. En esta sección, te explicaremos detalladamente cómo calcular el área de un trapecio en simples pasos.

Paso 1: Identificar los datos necesarios

Antes de comenzar a calcular el área del trapecio, debes asegurarte de tener todos los datos necesarios. Para calcular el área, necesitarás conocer la longitud de las bases del trapecio (base mayor y base menor) y la altura del trapecio.

Paso 2: Recordar la fórmula del área del trapecio

La fórmula para calcular el área de un trapecio es:

Area = (Base mayor + Base menor) * Altura / 2

Es importante recordar la fórmula y tenerla presente durante todo el proceso de cálculo.

Paso 3: Sustituir los valores en la fórmula

Una vez que tienes identificados los datos necesarios y recuerdas la fórmula del área del trapecio, puedes proceder a sustituir los valores en la fórmula.

Ingresa la longitud de la base mayor y base menor en sus respectivas variables, y la altura en su variable correspondiente.

Paso 4: Realizar los cálculos

Una vez que hayas sustituido los valores en la fórmula, puedes comenzar a realizar los cálculos. Asegúrate de utilizar correctamente las operaciones matemáticas, comenzando por la suma de las bases y multiplicando por la altura. Finalmente, divide el resultado entre 2.

Paso 5: Obtener el resultado

Una vez que hayas realizado los cálculos, obtendrás el resultado del área del trapecio. Asegúrate de redondear correctamente según la precisión necesaria y escribir la respuesta de forma clara y concisa.

Ahora que conoces los pasos para calcular el área de un trapecio, puedes practicar con diferentes ejemplos y adquirir mayor destreza en esta habilidad matemática. Recuerda siempre verificar tus resultados y seguir practicando para perfeccionar tus habilidades en matemáticas.

Qué información adicional se necesita para calcular el área de un trapecio si solo se conocen las bases

Para calcular el área de un trapecio, es necesario conocer tanto las bases como la altura del trapecio. Las bases son los lados paralelos del trapecio, mientras que la altura es la distancia perpendicular entre las bases.

Si solo se conocen las bases de un trapecio y no se tiene información adicional, no es posible determinar directamente el área. En estos casos, se necesita identificar valores adicionales, como la altura o algún otro lado o ángulo, para poder calcular el área de forma precisa.

Existen diferentes métodos para determinar la altura de un trapecio cuando solo se conocen las bases. Uno de ellos es utilizar teoremas de geometría, como el teorema de Pitágoras o el teorema de Tales, en combinación con las propiedades del trapecio.

Uso del teorema de Pitágoras

Si se conoce la longitud de los dos lados no paralelos de un trapecio isósceles, se puede utilizar el teorema de Pitágoras para encontrar la altura del trapecio.

El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de los otros dos lados. Aplicando esto al trapecio isósceles, se puede considerar uno de los lados no paralelos como la hipotenusa del triángulo rectángulo formado por esa base, la altura y la línea que une los puntos medios de las bases. Al resolver la ecuación resultante, se obtiene la altura del trapecio.

Uso del teorema de Tales

Otro método para determinar la altura de un trapecio cuando solo se conocen las bases es utilizando el teorema de Tales.

El teorema de Tales establece que si se traza una línea paralela a una base del trapecio desde uno de los vértices opuestos, se forman dos triángulos semejantes. Esto significa que las longitudes proporcionales de los lados de estos triángulos también serán proporcionales.

Si se conoce la longitud de la línea paralela trazada desde uno de los vértices opuestos y una de las bases del trapecio, mediante la aplicación del teorema de Tales es posible obtener la altura del trapecio. Esta altura será proporcional a la longitud de la línea trazada y se puede encontrar utilizando una simple regla de tres.

Una vez que se haya determinado la altura del trapecio, ya será posible utilizar la fórmula del área del trapecio, que consiste en multiplicar la suma de las bases por la altura y dividir el resultado entre 2.

Cómo se puede utilizar la altura de un trapecio para calcular su área

La altura de un trapecio es una medida importante para determinar su área. La fórmula del área de un trapecio se basa en la longitud de sus bases y en su altura.

Fórmula del área del trapecio

La fórmula general para calcular el área de un trapecio es:

Área = (base mayor + base menor) * altura / 2

• Área: representa el área del trapecio.
• Base mayor: es la longitud de la base superior del trapecio.
• Base menor: es la longitud de la base inferior del trapecio.
• Altura: es la distancia vertical entre las bases del trapecio.

Así, para calcular el área de un trapecio, simplemente necesitas conocer la longitud de sus bases y su altura.

Ejemplo práctico

Supongamos que tenemos un trapecio con una base mayor de 8 cm, una base menor de 4 cm y una altura de 6 cm. Podemos aplicar la fórmula del área del trapecio para calcular su área de la siguiente manera:

Área = (8 + 4) * 6 / 2

Resolviendo esta ecuación, obtenemos:

Área = 12 * 6 / 2
Área = 72 / 2
Área = 36 cm²

Por lo tanto, el área del trapecio en este ejemplo es de 36 cm².

Como puedes ver, utilizar la altura del trapecio en conjunto con las longitudes de sus bases nos permite calcular fácilmente su área utilizando la fórmula adecuada.

Consideraciones adicionales

Es importante recordar que las medidas de las bases y la altura deben estar expresadas en la misma unidad de medida para obtener un resultado correcto. Además, la altura debe ser perpendicular a ambas bases.

También es válido destacar que esta fórmula solo calcula el área de un trapecio y no toma en cuenta otras características relevantes como los ángulos o los lados inclinados. Por lo tanto, asegúrate de que los datos proporcionados sean consistentes con la definición de un trapecio antes de aplicar esta fórmula.

Ahora que conoces cómo usar la altura de un trapecio para calcular su área, puedes aplicar estos conocimientos a problemas y situaciones que involucren trapecios en tu vida cotidiana o en el estudio de las matemáticas.

Cuáles son algunos ejemplos prácticos de cómo calcular el área de un trapecio

Calcular el área de un trapecio puede parecer intimidante al principio, pero con la fórmula adecuada y algunos ejemplos prácticos, puede convertirse en una tarea mucho más sencilla. Aquí te presentaremos algunos ejemplos para que puedas aplicar y entender mejor cómo determinar esta medida.

Ejemplo 1: Área de un trapecio con bases paralelas

Supongamos que tenemos un trapecio con bases paralelas de longitudes 5 cm y 10 cm, y una altura de 8 cm. Para calcular su área, utilizaremos la fórmula:

A = (base mayor + base menor) * altura / 2

Sustituyendo los valores que tenemos, obtenemos:

A = (5 + 10) * 8 / 2
A = 15 * 8 / 2
A = 120 / 2
A = 60 cm²

Por lo tanto, el área de este trapecio es de 60 cm².

Ejemplo 2: Área de un trapecio con una base desconocida

A veces, podemos tener un trapecio en el que conocemos una base y la altura, pero no sabemos el valor de la otra base. En este caso, necesitamos utilizar otro método para calcular el área. Supongamos que tenemos un trapecio con una base de longitud 6 cm, una altura de 9 cm y la longitud de la otra base desconocida. Para determinarla, podemos utilizar la ecuación:

A = (base mayor + base menor) * altura / 2

Podemos aplicar esta fórmula y despejar la base desconocida (b2) de la siguiente manera:

A = (6 + b2) * 9 / 2
2A = (6 + b2) * 9
2A = 54 + 9b2
2A - 54 = 9b2
b2 = (2A - 54) / 9

Conociendo el valor del área (A), podemos calcular el ancho de la segunda base del trapecio. Una vez que hayamos encontrado ese valor, podemos usarlo junto con la fórmula original para determinar el área del trapecio.

Ejemplo 3: Área de un trapecio escaleno

Un trapecio escaleno es aquel en el que todas sus bases tienen diferentes longitudes. En este caso, no se puede asumir que las bases están paralelas entre sí. Supongamos que tenemos un trapecio con una base1 de longitud 12 cm, una base2 de longitud 8 cm y una altura de 5 cm. Para calcular su área, podemos usar nuevamente la fórmula:

A = (base mayor + base menor) * altura / 2

Sustituyendo los valores conocidos, obtenemos:

A = (12 + 8) * 5 / 2
A = 20 * 5 / 2
A = 100 / 2
A = 50 cm²

Entonces, el área de este trapecio escaleno es de 50 cm².

Estos ejemplos prácticos te ayudarán a comprender mejor cómo se puede calcular el área de un trapecio en diferentes situaciones. Recuerda siempre identificar las medidas conocidas y aplicar la fórmula correcta para obtener el valor del área deseada. ¡No dudes en practicar con más ejercicios e ir adquiriendo confianza en tus habilidades matemáticas!

Existen otras fórmulas alternativas para calcular el área de un trapecio

La fórmula más comúnmente utilizada para calcular el área de un trapecio es:

Área = (base mayor + base menor) * altura / 2

Sin embargo, existen otras fórmulas alternativas que también permiten determinar el área de un trapecio de manera precisa.

Fórmula utilizando la longitud de los lados y uno de los ángulos

Si conoces la longitud de los lados del trapecio (a y b) y uno de los ángulos laterales (α), puedes utilizar la siguiente fórmula:

Área = (a + b)* h / 2 = (a + b) * sin(α) / 2

Esta fórmula es especialmente útil cuando se tiene información sobre los lados y los ángulos de un trapecio y se desea calcular su área sin saber la longitud de las bases.

Fórmula utilizando la diagonal y la diferencia de las bases

Otra fórmula que puede ser utilizada para calcular el área de un trapecio es cuando se conoce la longitud de la diagonal del trapecio (d) y la diferencia entre las bases (b - a):

Área = ((b + a) / 2) * sqrt(d^2 - ((b - a)^2 / 4))

En esta fórmula, "sqrt" representa la función raíz cuadrada y "^" indica exponente.

Estas fórmulas ofrecen una alternativa al método tradicional y pueden ser útiles en diferentes situaciones donde se conocen diferentes datos sobre el trapecio.

Cuáles son algunos errores comunes que se deben evitar al calcular el área de un trapecio

Al calcular el área de un trapecio, es común cometer algunos errores que pueden llevar a resultados incorrectos. Para evitar caer en estas trampas matemáticas, es importante tener en cuenta los siguientes puntos:

1. No confundir la base mayor con la base menor

El trapecio es un polígono con dos bases: la base mayor y la base menor. Uno de los errores más comunes es confundir cuál es cuál al aplicar la fórmula del área del trapecio. Recuerda que la base mayor es la medida más larga del trapecio, mientras que la base menor es la medida más corta.

2. No olvidar dividir la suma de las bases entre 2

La fórmula del área del trapecio requiere sumar las medidas de las bases y multiplicar el resultado por la altura del trapecio. Sin embargo, uno de los errores más frecuentes es olvidarse de dividir esta suma entre 2. Esta división es necesaria para obtener el promedio de las bases y calcular correctamente el área.

3. No confundir la altura del trapecio con la longitud de los lados no paralelos

Otro error común al calcular el área de un trapecio es confundir la altura del trapecio con la longitud de los lados no paralelos. La altura del trapecio es la medida perpendicular a las bases, mientras que la longitud de los lados no paralelos corresponde a las distancias entre los puntos donde se encuentran las bases con los lados. Asegúrate de utilizar la altura correcta en la fórmula para obtener resultados precisos.

4. No redondear los números antes de calcular el área

Es importante evitar redondear las medidas de las bases y la altura del trapecio antes de aplicar la fórmula del área. Si se redondean prematuramente, se pueden introducir errores significativos en el resultado final. Realiza todos los cálculos con las medidas exactas y redondea solo al obtener el resultado final deseado.

5. No olvidar utilizar las unidades de medida adecuadas

Al calcular el área de un trapecio, es esencial recordar utilizar las mismas unidades de medida para todas las dimensiones involucradas. Si las bases están medidas en metros, la altura también debe estar en metros para que el resultado sea coherente. Cometer errores al mezclar diferentes unidades de medida puede llevar a resultados incorrectos.

Siguiendo estos consejos y evitando estos errores comunes, podrás calcular fácilmente el área de un trapecio de manera precisa y sin problemas matemáticos innecesarios.

La fórmula para calcular el área de un trapecio es: A = (b1 + b2) * h / 2

2) ¿Qué representan b1, b2 y h en la fórmula del área del trapecio?

b1 y b2 son las longitudes de las bases paralelas del trapecio, mientras que h es la altura del trapecio perpendicular a las bases.

3) ¿Puedo calcular el área de un trapecio si solo tengo las medidas de los lados?

No, para calcular el área de un trapecio necesitas conocer las medidas de las bases o la longitud de los lados no es suficiente.

4) ¿Cómo puedo medir la altura de un trapecio si no está marcada?

Puedes usar herramientas como una regla y un transportador para medir los ángulos y las longitudes de los lados. Luego, puedes utilizar trigonometría para encontrar la altura.

5) ¿Hay alguna forma más sencilla de calcular el área de un trapecio?

Sí, si el trapecio es isósceles, es decir, tiene dos lados iguales, puedes usar la fórmula simplificada: A = (b^2 * s) / 4, donde b es la base y s es uno de los lados iguales.