¡Descubre cuánto suman los ángulos de un triángulo! Aprende sobre esta fascinante propiedad geométrica y sorpréndete con los resultados

La geometría es una rama de las matemáticas que estudia las propiedades y las medidas de las figuras en el espacio. Uno de los temas más interesantes dentro de la geometría es el estudio de los triángulos, que son polígonos formados por tres segmentos de recta llamados lados.

Exploraremos una propiedad fundamental de los triángulos: la suma de los ángulos interiores. Aprenderemos cómo se calcula esta suma y descubriremos algunos resultados sorprendentes. Además, conoceremos las aplicaciones prácticas de esta propiedad en diferentes campos, como la arquitectura y la ingeniería.

Cuál es la propiedad geométrica que relaciona los ángulos de un triángulo

La propiedad geométrica que relaciona los ángulos de un triángulo se conoce como "la suma de los ángulos internos". Esta propiedad establece que, sin importar las medidas específicas de los ángulos de un triángulo, la suma de ellos siempre será igual a 180 grados.

Esta propiedad es una de las más fundamentales y conocidas en geometría. Desde la prueba más simple hasta teoremas más avanzados, la suma de los ángulos internos de un triángulo se utiliza como base para el estudio y resolución de problemas geométricos.

Cómo calcular la suma de los ángulos de un triángulo

Calcular la suma de los ángulos de un triángulo es bastante sencillo. Los triángulos tienen tres ángulos internos, a los que generalmente se les denota como ángulo A, ángulo B y ángulo C.

Para obtener la suma de los ángulos internos de un triángulo, simplemente sumamos las medidas de los tres ángulos:

Suma de ángulos internos = ángulo A + ángulo B + ángulo C

Por ejemplo, si tenemos un triángulo donde el ángulo A mide 50 grados, el ángulo B mide 70 grados y el ángulo C mide 60 grados, podemos calcular la suma de los ángulos de la siguiente manera:

Suma de ángulos internos = 50 grados + 70 grados + 60 grados
Suma de ángulos internos = 180 grados

Por lo tanto, la suma de los ángulos internos de este triángulo es igual a 180 grados, cumpliendo así con la propiedad geométrica mencionada anteriormente.

Cómo se puede calcular la suma de los ángulos de un triángulo

Calcular la suma de los ángulos de un triángulo es una tarea muy sencilla y fascinante en el mundo de la geometría. Esta propiedad geométrica ha sido estudiada por siglos y tiene aplicaciones clave en diversos campos, desde la arquitectura hasta la astronomía.

Para comprender cómo calcular la suma de los ángulos de un triángulo, es importante recordar que un triángulo es una figura plana compuesta por tres lados y tres ángulos. Estos ángulos pueden variar en medida y forma, pero siempre existe una relación constante entre ellos que permite calcular su suma total.

La propiedad fundamental que nos ayuda a calcular la suma de los ángulos de un triángulo se conoce como el Teorema de la Suma de los Ángulos de un Triángulo. Este teorema establece que la suma de los ángulos internos de cualquier triángulo siempre es igual a 180 grados (π radianes).

En otras palabras, si tomamos cualquier triángulo y medimos los tres ángulos internos con un transportador, al sumar estos ángulos obtendremos siempre el mismo resultado: 180 grados.

Esta propiedad geométrica puede demostrarse de varias maneras, utilizando diferentes métodos como el razonamiento deductivo o el uso de las propiedades de la paralelismo y congruencia de los ángulos.

Un ejemplo práctico

Supongamos que tenemos un triángulo ABC, donde los ángulos A, B y C corresponden a sus vértices respectivos. Podemos utilizar el teorema de la suma de los ángulos de un triángulo para calcular su suma.

<html>
  <head>
    <title>Suma de los ángulos de un triángulo</title>
  </head>
  <body>
    <h1>Triángulo ABC</h1>
    <p>Los ángulos del triángulo ABC son:</p>
    <ul>
      <li>Ángulo A = 60 grados</li>
      <li>Ángulo B = 30 grados</li>
      <li>Ángulo C = 90 grados</li>
    </ul>
    <p>La suma de los ángulos del triángulo ABC es: 60 + 30 + 90 = 180 grados</p>
  </body>
</html>

En este ejemplo, hemos utilizado una estructura básica de HTML para mostrar la información del triángulo ABC y calcular la suma de sus ángulos. Hemos utilizado etiquetas como <head>, <title>, <h1>, <p> y <ul> para organizar el contenido de manera legible y estructurada.

Al ejecutar este código, obtendríamos como resultado la visualización de los ángulos del triángulo ABC y su suma total de 180 grados.

Es importante tener en cuenta que esta propiedad es válida para cualquier tipo de triángulo: equilátero, isósceles o escaleno. Esto significa que independientemente de la forma o tamaño del triángulo, la suma de sus ángulos siempre será igual a 180 grados.

La propiedad de la suma de los ángulos de un triángulo tiene aplicaciones prácticas en diversas áreas de la vida cotidiana y la ciencia. Por ejemplo, en la arquitectura se utiliza para diseñar estructuras estables y proporcionales, mientras que en la astronomía se emplea para calcular la posición y trayectoria de los astros en el espacio.

Calcular la suma de los ángulos de un triángulo es una propiedad fundamental de la geometría que nos permite comprender y analizar las propiedades de esta figura geométrica tan común en nuestra realidad. A través del Teorema de la Suma de los Ángulos de un Triángulo, podemos determinar con certeza que la suma de los ángulos internos de cualquier triángulo siempre será igual a 180 grados.

Cuántos grados suman los ángulos de un triángulo equilátero

Un triángulo equilátero es aquel que tiene sus tres lados iguales y por lo tanto, sus tres ángulos también son iguales. Para calcular cuántos grados suman los ángulos de un triángulo equilátero, debemos dividir 180° (la suma total de los ángulos de cualquier triángulo) entre 3 (el número de ángulos).

Por lo tanto, tenemos la siguiente fórmula:

Suma de los ángulos de un triángulo equilátero = 180° / 3 = 60°

Así que en un triángulo equilátero, cada uno de los ángulos interiores mide exactamente 60 grados.

Qué sucede con la suma de los ángulos de un triángulo isósceles

Un triángulo isósceles es aquel que tiene dos lados de igual longitud y dos ángulos iguales. La propiedad más fascinante de este tipo de triángulo es la relación entre la medida de sus ángulos.

Para calcular la suma de los ángulos de un triángulo isósceles, primero debemos conocer la medida de uno de sus ángulos. Supongamos que uno de los ángulos del triángulo isósceles mide x grados. Dado que los otros dos ángulos son iguales, también medirán x grados cada uno.

Utilizando la fórmula para calcular la suma de los ángulos de un triángulo, sabemos que:

x + x + x = 180°

Simplificando la ecuación, obtenemos:

3x = 180°

Ahora, despejando x, podemos encontrar la medida de cada ángulo:

x = 180° / 3

Resolviendo la ecuación, encontramos que:

x = 60°

Por lo tanto, cada ángulo de un triángulo isósceles mide 60 grados, y la suma de los ángulos es igual a:

60° + 60° + 60° = 180°

Así, hemos demostrado que los ángulos de un triángulo isósceles siempre suman 180 grados.

Y qué ocurre con la suma de los ángulos de un triángulo escaleno

El triángulo escaleno es aquel en el que sus tres lados tienen longitudes diferentes entre sí. A diferencia del triángulo equilátero o isósceles, los ángulos internos de un triángulo escaleno pueden ser diferentes y no existe ninguna simetría especial.

Entonces, ¿cuánto suman los ángulos de un triángulo escaleno? Veamos:

Primero, asignemos una letra a cada uno de los ángulos del triángulo escaleno. Podemos utilizar las letras A, B y C.
A continuación, recordemos que la suma de todos los ángulos de cualquier polígono siempre equivale a 180 grados.

Ahora, vamos a establecer una relación entre los ángulos de un triángulo escaleno utilizando la suma de los ángulos interiores. Para ello, utilizaremos la siguiente fórmula:

Suma de los ángulos = Ángulo A + Ángulo B + Ángulo C

Si queremos encontrar la suma de los ángulos de un triángulo en específico, simplemente debemos sustituir los valores correspondientes a los ángulos A, B y C en la fórmula e realizar la operación matemática necesaria. Por ejemplo:

Suma de los ángulos = 30° + 75° + 55°

Realizando la operación tenemos:

Suma de los ángulos = 160°

Por lo tanto, en este caso particular, la suma de los ángulos de un triángulo escaleno es igual a 160 grados.

Es importante destacar que este resultado puede variar en cada triángulo escaleno dependiendo de los valores de los ángulos A, B y C. Sin embargo, la suma siempre será igual a 180 grados debido a la propiedad común a todos los polígonos.

Asimismo, cabe mencionar que la suma de los ángulos internos de cualquier triángulo siempre será menor a 360 grados, ya que si se sobrepasara dicho valor, estaríamos ante un polígono con más lados.

Por qué siempre se obtiene el mismo resultado al sumar los ángulos internos de un triángulo

Los triángulos son figuras geométricas fascinantes que han capturado la atención de matemáticos y científicos desde tiempos antiguos. Una de las propiedades más sorprendentes de los triángulos es que la suma de sus ángulos internos siempre es igual a un valor constante, independientemente de su forma o tamaño.

Para entender por qué esto ocurre, es importante conocer algunos conceptos básicos de geometría. En primer lugar, recordemos que un triángulo está compuesto por tres lados y tres ángulos. Los ángulos internos de un triángulo son aquellos que se encuentran dentro de la figura, mientras que los ángulos externos son aquellos que se forman al extender los lados del triángulo hacia afuera.

En geometría euclidiana, se define que la suma de los ángulos internos de un triángulo es siempre igual a 180 grados. Esto significa que si medimos los ángulos internos de cualquier triángulo y sumamos sus medidas en grados, obtendremos siempre el mismo resultado: 180 grados.

La demostración matemática de esta propiedad

La propiedad de la suma de los ángulos internos de un triángulo puede ser demostrada utilizando razonamientos geométricos y algebraicos. Una posible demostración consiste en considerar un triángulo cualquiera y dividirlo en dos triángulos más pequeños mediante una línea que pase por uno de los vértices.


  // Demostración de la propiedad de la suma de ángulos internos de un triángulo
  let angulo1 = 60; // Primer ángulo del triángulo
  let angulo2 = 80; // Segundo ángulo del triángulo

  // Calculamos el tercer ángulo restando la suma de los dos ángulos anteriores a 180 grados
  let angulo3 = 180 - (angulo1 + angulo2);

  // Tomando en cuenta que la suma de los ángulos internos debe ser igual a 180, imprimimos el resultado
  console.log("El tercer ángulo es: " + angulo3 + "");

En este ejemplo, supongamos que tenemos un triángulo con un ángulo de 60 grados y otro ángulo de 80 grados. Para encontrar el tercer ángulo, podemos restar la suma de los dos ángulos conocidos a 180 grados. Esto nos dará un tercer ángulo de 40 grados.

Si realizamos esta demostración con diferentes valores para los ángulos del triángulo, siempre obtendremos el mismo resultado: la suma de los ángulos internos será igual a 180 grados. Esta propiedad se cumple para todo tipo de triángulos, ya sean equiláteros, isósceles o escalenos.

Es importante destacar que esta propiedad solo se aplica a triángulos planos en geometría euclidiana. En otras ramas de la geometría no euclidiana, como la geometría esférica o hiperbólica, esta propiedad puede no ser válida.

La suma de los ángulos internos de un triángulo es una propiedad matemática fascinante que siempre se cumple en geometría euclidiana. Esta propiedad ha sido estudiada y demostrada a lo largo de la historia de las matemáticas, y su comprensión nos permite entender mejor las propiedades y características de los triángulos.

Preguntas frecuentes (FAQ)

1. ¿Cuánto suman los ángulos de un triángulo?

Los ángulos de un triángulo siempre suman 180 grados.

2. ¿Todos los triángulos tienen la misma suma de ángulos?

Sí, independientemente del tipo de triángulo (equilátero, isósceles o escaleno), la suma de sus ángulos será siempre igual a 180 grados.

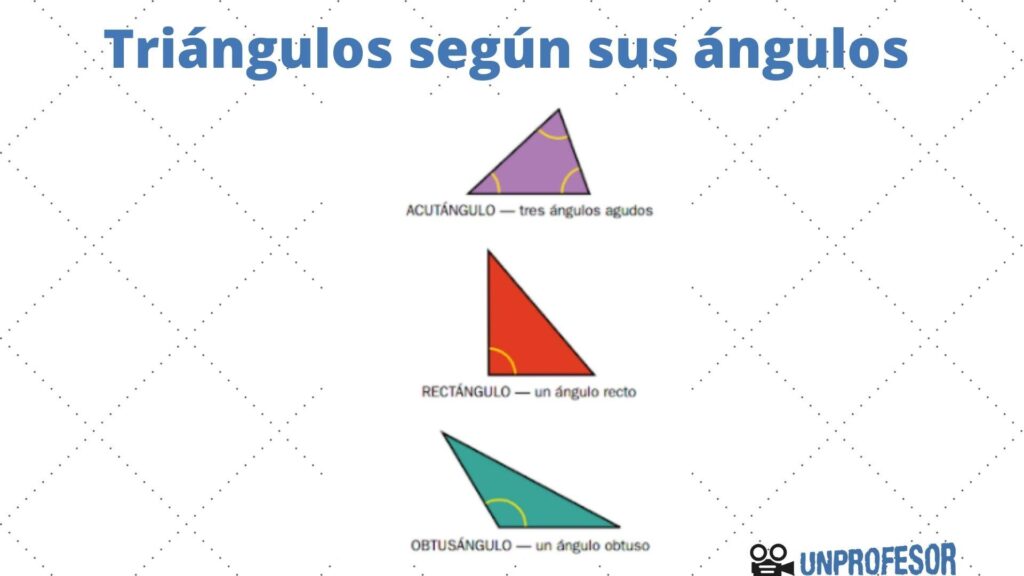
3. ¿Es posible que un triángulo tenga un ángulo recto y otros dos ángulos agudos?

Sí, esto es posible. Se trata de un tipo de triángulo llamado triángulo rectángulo.

4. ¿Qué características tiene un triángulo equilátero en cuanto a sus ángulos?

Un triángulo equilátero tiene todos sus ángulos iguales y miden 60 grados cada uno.

5. ¿Existe algún tipo de triángulo en el que la suma de sus ángulos sea mayor a 180 grados?

No, la suma de los ángulos internos de cualquier triángulo siempre será igual a 180 grados.

Entradas relacionadas

Deja una respuesta Cancelar la respuesta