Descubre la esencia de un vértice en geometría: Aprende qué es y por qué es fundamental para entender figuras y formas

La geometría es una rama de las matemáticas que se encarga del estudio de las formas, los tamaños y las propiedades del espacio. Una de las nociones fundamentales en geometría son los vértices, que juegan un papel vital en la definición de figuras geométricas.

Exploraremos qué es un vértice en geometría, cómo se define y cuál es su importancia en el análisis de formas y figuras. También veremos algunos ejemplos de cómo se identifican los vértices en diferentes tipos de figuras geométricas. ¡Prepárate para sumergirte en el fascinante mundo de los vértices!

Qué es un vértice en geometría y cómo se define

Un vértice en geometría es un punto de intersección entre dos o más líneas, segmentos o rayos. Es el lugar geométrico donde convergen estas entidades y se encuentran en un solo punto.

En términos más precisos, un vértice puede definirse como la intersección de dos aristas en una figura tridimensional, como un polígono o un poliedro. En el caso de las figuras planas, como los triángulos o los cuadriláteros, un vértice es el punto de encuentro de dos o más segmentos o lados.

Es importante destacar que un vértice no posee longitud, anchura ni altura, ya que se trata de un punto en el espacio. Sin embargo, su ubicación determina las características y propiedades de una figura geométrica, lo cual resulta fundamental para comprender su estructura y forma.

Cuál es la importancia de los vértices en la geometría

Los vértices son elementos fundamentales en la geometría que nos permiten definir y entender las distintas figuras y formas que existen.

Un vértice es el punto de intersección de dos o más segmentos, líneas o rayos en un plano o en el espacio tridimensional. Es el lugar donde convergen las diferentes partes de una figura geométrica, como los lados de un polígono o las aristas de un sólido.

La importancia de los vértices radica en que son los puntos clave para determinar propiedades y características de las figuras geométricas. A través de ellos podemos identificar y describir aspectos como:

• El número de vértices de una figura: conocer el número de vértices nos permite clasificar las figuras y comprender su estructura.
• Las dimensiones de una figura: los vértices son esenciales para determinar si una figura es bidimensional o tridimensional.
• Los ángulos y las rectas: los vértices son puntos de encuentro de líneas rectas, por lo que nos ayudan a medir y calcular los ángulos formados.
• La simetría: a través de los vértices, podemos identificar si una figura tiene simetría y qué tipo de simetría posee.

La presencia de los vértices en las figuras geométricas nos proporciona información valiosa sobre sus propiedades y características. Su estudio y comprensión son fundamentales para el desarrollo de la geometría y su aplicación en diversas áreas del conocimiento.

Cómo se identifican los vértices en diferentes figuras geométricas

En geometría, un vértice es un punto donde se encuentran dos o más líneas, segmentos o rayos. Es fundamental identificar y comprender los vértices para entender y trabajar con diferentes figuras y formas geométricas.

Para identificar los vértices en figuras geométricas regulares y polígonos, simplemente buscaremos los puntos donde las líneas o los segmentos se intersectan. Por ejemplo, en un triángulo equilátero, los tres puntos de intersección de los lados son los vértices del triángulo. En un cuadrado, los cuatro puntos de intersección de los lados también son los vértices del cuadrado.

En figuras geométricas más complejas como los polígonos irregulares y los sólidos tridimensionales, la identificación de los vértices puede ser un poco más desafiante. En este caso, necesitamos buscar puntos de intersección entre líneas, aristas o caras para encontrar los vértices.

Ejemplos de identificación de vértices

Veamos algunos ejemplos para entender cómo se identifican los vértices en diferentes figuras geométricas:

1. Triángulo escaleno: Un triángulo con todos sus lados de diferente longitud. Los puntos de intersección de los lados son los vértices del triángulo.

    
       A
      / 
     /   
    B-----C
    
  

En este ejemplo, los puntos A, B y C son los vértices del triángulo escaleno.

2. Cuadrado: Un polígono de cuatro lados iguales y ángulos rectos. Los puntos de intersección de los lados son los vértices del cuadrado.

    
     A------B
     |      |
     |      |
     C------D
    
  

Aquí, los puntos A, B, C y D son los vértices del cuadrado.

3. Cubo: Un sólido tridimensional con seis caras cuadradas idénticas. Los puntos de intersección de las aristas son los vértices del cubo.

    
         E-------F
        /|      /|
       / |     / |
      A--|----B  |
      |  G----|--H
      | /     | /
      |/      |/
      C-------D
    
  

En este caso, los puntos E, F, A, B, G, H, C y D son los vértices del cubo.

Como podemos ver en estos ejemplos, los vértices son puntos clave que nos permiten definir y describir las características principales de las figuras geométricas. Su identificación es fundamental para entender la estructura y las propiedades de estas figuras, y así poder realizar cálculos y resolver problemas relacionados con ellas.

Cuál es la relación entre los vértices y otras características geométricas, como los lados y las aristas

Los vértices son puntos de intersección en una figura geométrica. Estos puntos definen las esquinas y los ángulos de la figura. Cada figura geométrica tiene una cantidad específica de vértices, que se relaciona con el número de lados y aristas que posee.

En el caso de los polígonos, como los triángulos y los cuadriláteros, cada vértice se corresponde con un segmento de línea recta que representa un lado de la figura. Por ejemplo, un triángulo equilátero tiene tres vértices, ya que tiene tres lados. Un cuadrado tiene cuatro vértices, uno en cada esquina, que coinciden con los cuatro lados del cuadrado.

Por otro lado, las figuras tridimensionales, como los prismas y los sólidos de Platón, también tienen vértices. Sin embargo, en este caso, los vértices representan los puntos donde se encuentran diferentes caras o planos de la figura. Cada vértice está conectado a varias aristas, que son segmentos de línea que representan los bordes de las caras adyacentes.

Los vértices están directamente relacionados con los lados y aristas de una figura geométrica. La cantidad de vértices coincide con el número de lados en los polígonos y con los puntos de intersección entre las caras en las figuras tridimensionales.

Cuántos vértices tiene una figura geométrica en particular

Una figura geométrica puede tener diferentes cantidad de vértices dependiendo de su forma y dimensionalidad.

Vértices en figuras de dos dimensiones

En las figuras de dos dimensiones, también conocidas como figuras planas, el número de vértices está directamente relacionado con el número de lados de la figura.

Por ejemplo, un triángulo tiene tres lados y, por lo tanto, tres vértices. Si consideramos un cuadrado, este tiene cuatro lados y, consecuentemente, cuatro vértices. El número de vértices siempre será igual al número de lados en una figura de dos dimensiones.

Vértices en figuras de tres dimensiones

Las figuras de tres dimensiones, también conocidas como sólidos, tienen un número más variado de vértices debido a la mayor cantidad de aristas y caras que las componen.

Para entender la relación entre los vértices, las aristas y las caras en un sólido, podemos recurrir a la fórmula de Euler: V + F = A + 2, donde V es el número de vértices, F el número de caras y A el número de aristas del sólido.

Por ejemplo, si consideramos un cubo, que tiene 6 caras y 12 aristas, podemos reorganizar la fórmula de Euler para determinar el número de vértices:
V = A + 2 - F
Sustituyendo los valores conocidos:
V = 12 + 2 - 6 = 8
Entonces, el cubo tiene 8 vértices.

Esta fórmula se puede aplicar a cualquier sólido y nos brinda una manera de calcular el número de vértices sabiendo cuántas caras y aristas tiene.

Importancia de los vértices en la geometría

Los vértices son fundamentales en la geometría ya que, junto con las aristas y las caras, son los elementos básicos que definen una figura o forma. Los vértices determinan la forma y la estructura de un objeto y son la base para realizar cálculos como el área, el perímetro, el volumen, entre otros.

Además, los vértices son puntos clave en muchas propiedades y teoremas geométricos. Por ejemplo, en un triángulo, los vértices son utilizados para definir los ángulos internos y externos, así como para determinar si un triángulo es equilátero, isósceles o escaleno.

Tener un buen entendimiento de los vértices es esencial para desarrollar habilidades geométricas y poder analizar y describir figuras y formas de una manera precisa y rigurosa.

Cuáles son algunas aplicaciones prácticas de los vértices en el mundo real

Los vértices son elementos fundamentales en la geometría y su comprensión esencial permite entender la estructura y forma de objetos físicos y abstractos. La presencia de los vértices se puede observar en numerosas aplicaciones prácticas en el mundo real, desde la arquitectura hasta las ciencias de la computación.

Arquitectura y diseño

En el campo de la arquitectura y el diseño, los vértices son utilizados para determinar puntos de convergencia en la construcción de edificaciones. Los planos arquitectónicos y los diseños urbanos dependen de manera crucial de la ubicación precisa de los vértices para lograr estructuras estables y equilibradas. Además, los vértices son utilizados en la creación de moldes y patrones para la fabricación de elementos arquitectónicos y decorativos, permitiendo obtener formas precisas y simétricas.

Gráficos por computadora

En el campo de los gráficos por computadora, los vértices juegan un papel fundamental en la representación visual de objetos tridimensionales. Mediante la técnica conocida como "rendering", los vértices son utilizados para definir los puntos donde se intersectan las líneas que forman superficies tridimensionales, permitiendo así crear modelos digitales con profundidad y realismo. Esto es especialmente importante en la industria de los videojuegos, donde los vértices son utilizados para crear personajes, escenarios y efectos visuales impactantes.

Física y matemáticas

En el campo de la física y las matemáticas, los vértices son utilizados para describir y analizar la geometría de objetos abstractos. Por ejemplo, en el estudio de grafos y redes, los vértices representan puntos de conexión o nodos, mientras que las aristas representan las conexiones entre ellos. Esta representación gráfica es ampliamente utilizada en el análisis de sistemas complejos como las redes de transporte, las redes sociales y los sistemas de comunicación.

Música y arte

En la música y el arte, los vértices pueden ser interpretados como puntos de inflexión en una composición o una obra visual. La ubicación estratégica de los vértices puede generar sensaciones de tensión, equilibrio o movimiento dentro de una pieza artística. Además, en la creación de esculturas y obras tridimensionales, los vértices son utilizados para determinar la forma y estructura de la pieza, permitiendo así crear formas complejas y dinámicas.

Análisis de datos y machine learning

En el ámbito del análisis de datos y el machine learning, los vértices son utilizados para representar variables o características en un modelo matemático. Esto permite analizar patrones y relaciones entre diferentes variables para extraer información significativa. Por ejemplo, en la detección de comunidades en redes sociales, los vértices representan usuarios individuales y las aristas representan sus conexiones mutuas, lo que permite identificar grupos o comunidades con intereses comunes.

Cómo se puede calcular la coordenada de un vértice a través de sus puntos

En geometría, un vértice se define como el punto de intersección de dos o más segmentos de recta. Es uno de los elementos fundamentales para entender la forma y estructura de figuras geométricas, así como también para realizar cálculos y determinar propiedades matemáticas.

Para calcular la coordenada de un vértice a través de sus puntos, es importante tener en cuenta los siguientes pasos:

1. Identificar los puntos que forman el vértice: Para ello, es necesario conocer las coordenadas de los puntos que se intersectan. Estos puntos pueden representarse como (x₁, y₁) y (x₂, y₂).
2. Determinar la fórmula para calcular la coordenada del vértice: En función de los puntos identificados, puede utilizarse la fórmula x = (x₁ + x₂) / 2 y y = (y₁ + y₂) / 2 para obtener la coordenada del vértice.
3. Sustituir los valores de los puntos en la fórmula: Una vez conocidos los valores de x₁, x₂, y₁ y y₂, se reemplazan en la fórmula para calcular la coordenada del vértice.
4. Evaluar la fórmula y obtener el resultado: Al sustituir los valores de los puntos en la fórmula, se realiza la operación aritmética correspondiente para obtener el valor de x y y de la coordenada del vértice.

Es importante mencionar que este cálculo es válido para encontrar la coordenada de un vértice que se forma a partir de la intersección de dos segmentos de recta. En caso de tener un polígono con más de dos lados, se deben seguir otros procedimientos para calcular las coordenadas de sus vértices.

Calcular la coordenada de un vértice a través de sus puntos implica identificar los puntos que forman el vértice, determinar la fórmula correspondiente y sustituir los valores de los puntos para obtener el resultado. Este proceso matemático es fundamental para comprender la geometría y la relación entre los elementos que conforman las figuras y formas geométricas.

De qué manera los vértices influyen en la simetría de una figura geométrica

En geometría, un vértice es un punto donde se encuentran dos o más segmentos de una figura geométrica. Estos puntos de intersección son fundamentales para comprender la forma y la simetría de dicha figura.

Cuando una figura tiene un vértice, se crea un cambio de dirección en sus segmentos. Esto puede ser evidente en formas como los triángulos, cuadrados, pentágonos, etc. Al tener un vértice, estos polígonos pueden mostrar distintos ángulos y longitudes de sus lados.

¿Por qué es importante entender los vértices?

Los vértices son elementos clave en la geometría, ya que permiten describir las propiedades de las figuras y determinar su simetría. Comprender cómo funcionan los vértices puede ayudarnos a visualizar mejor las figuras y también a resolver problemas relacionados con ellas.

La simetría de una figura está estrechamente relacionada con la ubicación y cantidad de vértices que posee. Una figura puede tener uno o varios vértices, y dependiendo de esto, su simetría puede variar.

Por ejemplo, un cuadrado tiene cuatro vértices ubicados en las intersecciones de sus lados. Debido a esta característica, el cuadrado es una figura geométrica simétrica, lo que significa que se puede dividir en mitades iguales que se reflejan perfectamente una sobre la otra.

En contraste, un triángulo equilátero solo tiene tres vértices, por lo que su simetría es diferente a la del cuadrado. Aunque el triángulo equilátero también tiene un eje de simetría, solo se puede dividir en dos partes iguales, ya que no posee más vértices para lograr una simetría más compleja.

Al entender el papel de los vértices en la simetría de las figuras, podemos analizar y clasificar diferentes geometrías, lo que nos brinda herramientas para resolver problemas geométricos y armar estructuras con precisión.

Los vértices son puntos de intersección en una figura geométrica que influyen directamente en su simetría. Entender cómo funcionan los vértices nos permite comprender mejor las propiedades de las figuras, así como solucionar problemas relacionados con ellas.

Qué ejemplos emblemáticos de figuras geométricas destacan por tener múltiples vértices

En geometría, un vértice es un punto de encuentro entre dos o más segmentos de línea, rayos o líneas. Es una esencia fundamental para entender figuras y formas, ya que los vértices nos permiten definir las características y propiedades de las figuras geométricas.

Existen diversos ejemplos emblemáticos de figuras geométricas que destacan por tener múltiples vértices. A continuación, mencionaremos algunos de ellos:

1. El triángulo

El triángulo es una figura geométrica con tres lados y tres vértices. Cada uno de los vértices del triángulo es el punto de encuentro de dos de sus lados. Los vértices del triángulo son fundamentales para determinar la forma, tamaño y tipo de triángulo que estamos estudiando.

2. El cuadrado

El cuadrado es un polígono de cuatro lados iguales y cuatro ángulos rectos. Tiene cuatro vértices, cada uno de los cuales es el punto de encuentro de dos de sus lados. Los vértices del cuadrado son esenciales para determinar su posición en el plano y para calcular su perímetro y área.

3. El pentágono regular

El pentágono regular es un polígono de cinco lados y cinco ángulos iguales. Tiene cinco vértices, y cada uno de ellos es el punto de encuentro de dos de sus lados. Los vértices del pentágono regular son fundamentales para describir su forma y para calcular medidas como su perímetro y área.

4. El hexágono regular

El hexágono regular es un polígono de seis lados iguales y seis ángulos iguales. Tiene seis vértices, y cada uno de ellos es el punto de encuentro de dos de sus lados. Los vértices del hexágono regular son importantes para definir su forma y para realizar cálculos relacionados con su perímetro y área.

5. El octógono regular

El octógono regular es un polígono de ocho lados iguales y ocho ángulos iguales. Tiene ocho vértices, y cada uno de ellos es el punto de encuentro de dos de sus lados. Los vértices del octógono regular son fundamentales para determinar su estructura y para calcular medidas como su perímetro y área.

Estos son solo algunos ejemplos emblemáticos de figuras geométricas que destacan por tener múltiples vértices. Cada uno de estos vértices tiene un papel crucial en la definición y caracterización de las figuras, permitiéndonos comprender mejor sus atributos y propiedades matemáticas.

Un vértice es el punto donde se encuentran dos o más segmentos, líneas o rayos en una figura geométrica.

Identificar los vértices nos ayuda a comprender la estructura y forma de una figura, así como a calcular sus propiedades geométricas.

Un triángulo tiene tres vértices.

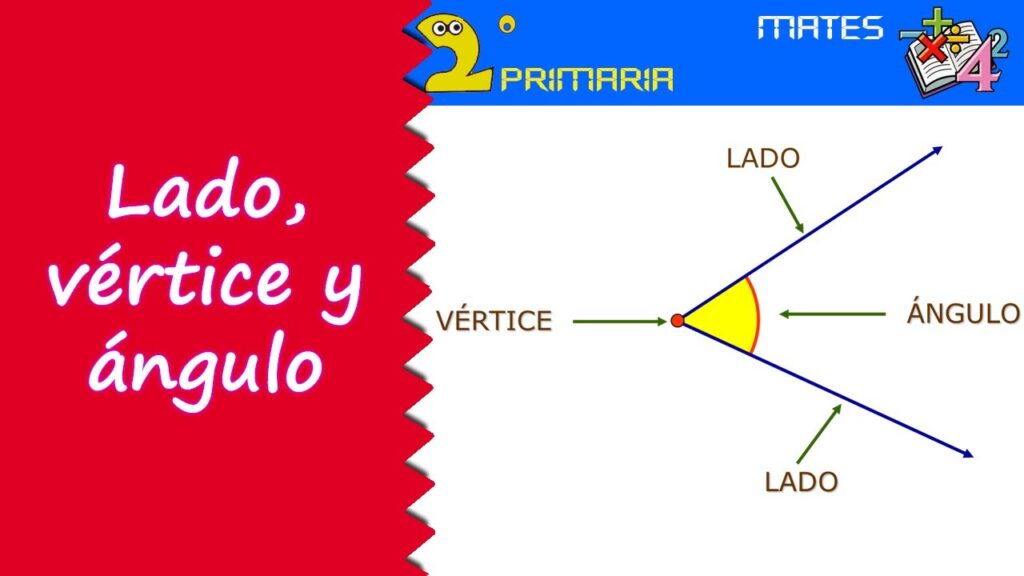
Un vértice es el punto de intersección de dos o más segmentos o líneas, mientras que un ángulo es la abertura entre dos líneas.

No, una línea recta no puede tener vértices porque no hay intersección de segmentos o líneas en ella.