Descubre qué es el Estadístico de Prueba y cómo impacta tus investigaciones

Cuando hablamos de investigación y análisis de datos, es común encontrarnos con términos como "estadístico de prueba". Pero, ¿qué significa realmente este concepto y cómo impacta en nuestras investigaciones? El estadístico de prueba es una herramienta fundamental en la estadística inferencial, que nos permite tomar decisiones sobre una hipótesis planteada.

Vamos a explorar en qué consiste el estadístico de prueba y cómo se calcula. Además, veremos cómo se utiliza para comparar un valor observado con un valor esperado y determinar si hay una diferencia significativa o no. También analizaremos la importancia de elegir correctamente el nivel de significancia y entender los errores tipo I y tipo II en la toma de decisiones. ¡Prepárate para adentrarte en el mundo de los estadísticos de prueba y su impacto en tus investigaciones!

Qué es el Estadístico de Prueba y por qué es importante en las investigaciones

El Estadístico de Prueba es una medida utilizada en el campo de la estadística para evaluar la evidencia en contra de una hipótesis nula. En otras palabras, se utiliza para determinar si los resultados obtenidos en una investigación son lo suficientemente diferentes como para rechazar la hipótesis nula y aceptar la hipótesis alternativa.

El Estadístico de Prueba se calcula utilizando los datos recopilados durante un estudio o experimento y se compara con un valor crítico predefinido, basado en el nivel de significancia elegido para el estudio. Si el valor calculado del Estadístico de Prueba supera el valor crítico, se considera que hay evidencia suficiente para rechazar la hipótesis nula y aceptar la hipótesis alternativa.

Es importante tener en cuenta que el Estadístico de Prueba no proporciona información sobre la magnitud o relevancia práctica de los resultados obtenidos. Simplemente indica si los resultados son estadísticamente significativos o no. Por lo tanto, es fundamental interpretar los resultados del Estadístico de Prueba en el contexto de la pregunta de investigación planteada y los objetivos del estudio.

Cómo se calcula el Estadístico de Prueba

El cálculo del Estadístico de Prueba depende del tipo de prueba estadística utilizada en el estudio. Existen diferentes pruebas estadísticas, como la prueba t de Student, la prueba chi-cuadrado y la prueba de ANOVA, entre otras.

En general, el Estadístico de Prueba se calcula dividiendo una diferencia entre grupos o una medida de asociación entre variables por una estimación de la variabilidad dentro de los grupos o las variables. Esta división es lo que permite evaluar la probabilidad de obtener un resultado tan extremo o más extremo si la hipótesis nula fuese cierta.

El cálculo exacto del Estadístico de Prueba varía según el tipo de prueba estadística utilizada, pero en todos los casos se sigue un enfoque similar: se definen las hipótesis nula y alternativa, se selecciona el nivel de significancia, se recopilan los datos relevantes y se aplica la fórmula correspondiente para calcular el Estadístico de Prueba.

Importancia del Estadístico de Prueba en las investigaciones

El Estadístico de Prueba desempeña un papel fundamental en las investigaciones científicas, ya que proporciona una herramienta objetiva para tomar decisiones basadas en evidencia y evaluar la validez de las conclusiones obtenidas.

A través del uso del Estadístico de Prueba, los investigadores pueden determinar si sus resultados son significativos desde un punto de vista estadístico, lo que les permite inferir relaciones causales y generalizar los hallazgos a una población objetivo más amplia. Además, el Estadístico de Prueba también permite evaluar la precisión y confiabilidad de los resultados, ayudando a asegurar que cualquier conclusión extraída sea sólida y respaldada por la evidencia recolectada.

El Estadístico de Prueba es una herramienta esencial para cualquier investigación científica, ya que proporciona una forma sistemática y objetiva de evaluar los resultados obtenidos y tomar decisiones basadas en evidencia. Su uso adecuado y una interpretación cuidadosa pueden garantizar la validez y relevancia de las conclusiones extraídas, contribuyendo al avance del conocimiento en diversas áreas de estudio.

Cuál es la relación entre el Estadístico de Prueba y la hipótesis nula

El estadístico de prueba es una medida que se utiliza en la inferencia estadística para evaluar qué tan probable es obtener los resultados observados, suponiendo que la hipótesis nula sea verdadera. La hipótesis nula (H0) es una afirmación que generalmente se plantea con el propósito de ser refutada.

En otras palabras, el estadístico de prueba nos permite calcular un valor numérico que refleja la discrepancia entre los datos observados y los esperados bajo la hipótesis nula. Con este valor, podemos determinar si la diferencia encontrada entre los datos es significativa o simplemente producto del azar.

La relación entre el estadístico de prueba y la hipótesis nula se establece a través de la distribución de probabilidad asociada al estadístico. Esta distribución nos indica la probabilidad de obtener valores del estadístico tan extremos o más extremos que el observado, si la hipótesis nula es cierta.

Cómo funciona el cálculo del estadístico de prueba

El cálculo del estadístico de prueba depende del tipo de prueba estadística que se esté realizando. Por ejemplo, en pruebas de hipótesis para la media poblacional, se utiliza el estadístico t de Student. Mientras que en pruebas para la proporción poblacional, se utiliza el estadístico Z.

Estadístico t de Student = (Media muestral - Media poblacional) / Error estándar de la media
Estadístico Z = (Proporción muestral - Proporción poblacional) / Error estándar de la proporción

El cálculo del estadístico de prueba implica obtener los valores relevantes a partir de la muestra y compararlos con los parámetros poblacionales establecidos en la hipótesis nula. Estos parámetros pueden ser una media poblacional, una proporción poblacional u otras medidas de interés según el contexto de la investigación.

Cómo interpretar el valor del estadístico de prueba

Una vez calculado el valor del estadístico de prueba, se compara con un valor crítico o se utiliza para calcular un p-valor. El valor crítico es un umbral preestablecido que se compara con el estadístico para determinar si existe evidencia suficiente para rechazar la hipótesis nula.

En cambio, el p-valor es la probabilidad de obtener un estadístico de prueba igual o más extremo que el observado, suponiendo que la hipótesis nula es cierta. Si el p-valor es menor que un nivel de significancia predefinido (usualmente 0.05), se considera que hay evidencia suficiente para rechazar la hipótesis nula.

El valor del estadístico de prueba nos indica qué tan lejos están los datos observados de lo que esperaríamos bajo la hipótesis nula. Dependiendo de su valor y de las pruebas adicionales realizadas, podemos tomar decisiones sobre si aceptar o rechazar la hipótesis nula, y así determinar el impacto de nuestras investigaciones.

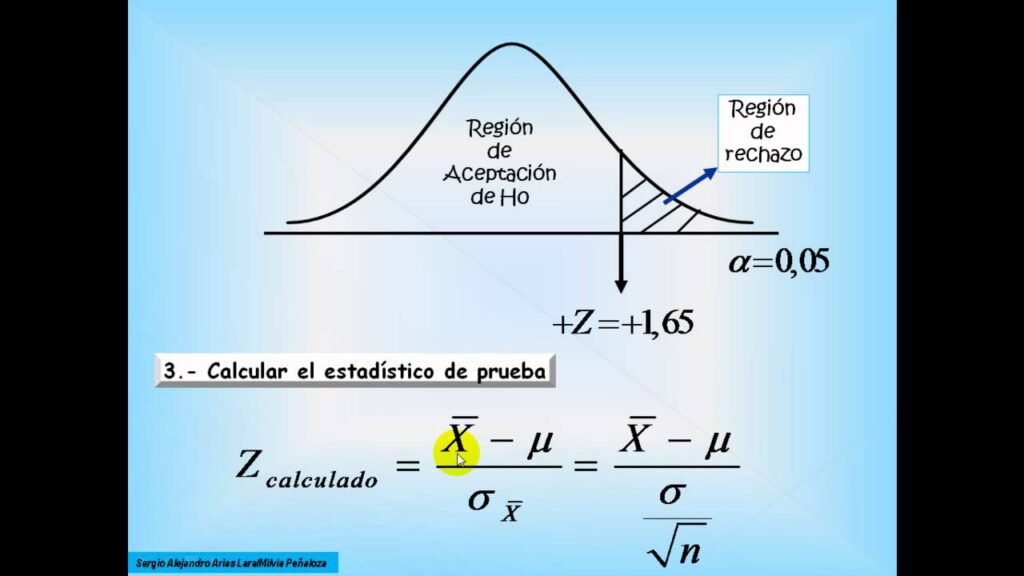
Cómo se calcula el Estadístico de Prueba en diferentes escenarios de investigación

El Estadístico de Prueba es una medida utilizada en el campo de la estadística para determinar si hay evidencia suficiente para rechazar o no una hipótesis nula en un experimento o estudio. Su cálculo varía dependiendo del tipo de prueba estadística que se esté realizando y del diseño del estudio.

Pruebas paramétricas

En las pruebas paramétricas, se asume que los datos siguen una distribución específica, como la distribución normal. Algunas de las pruebas paramétricas más comunes incluyen la prueba t, la prueba Z y el análisis de varianza (ANOVA). En estos casos, el Estadístico de Prueba se calcula tomando la diferencia entre la media observada y la media esperada bajo la hipótesis nula, y luego se divide por la desviación estándar de la muestra. El resultado obtenido sigue una distribución conocida que permite determinar si la diferencia es estadísticamente significativa.

Pruebas no paramétricas

En contraste, las pruebas no paramétricas no requieren supuestos sobre la distribución de los datos. Se utilizan cuando los datos no cumplen con los requisitos necesarios para realizar pruebas paramétricas. Algunos ejemplos de pruebas no paramétricas son la prueba de Mann-Whitney y la prueba de Wilcoxon. Para calcular el Estadístico de Prueba en estas pruebas, se asigna un rango a cada una de las observaciones y se compara la suma de rangos obtenida con una tabla de valores críticos. Si la suma de rangos es mayor o menor que el valor crítico, se rechaza la hipótesis nula.

Pruebas de correlación y regresión

En las pruebas de correlación y regresión, el Estadístico de Prueba se utiliza para determinar si hay una relación significativa entre dos o más variables. Algunas de las pruebas más comunes son la prueba de correlación de Pearson y la prueba de regresión lineal. En estos casos, el Estadístico de Prueba se calcula mediante la comparación de los coeficientes de correlación estimados con sus errores estándar. Si el valor del Estadístico de Prueba es lo suficientemente grande, se puede inferir que existe una relación estadísticamente significativa entre las variables.

El cálculo del Estadístico de Prueba varía dependiendo del tipo de prueba estadística que se esté realizando y del diseño del estudio. Tanto en las pruebas paramétricas como no paramétricas, se busca determinar si la diferencia observada es estadísticamente significativa, permitiendo tomar decisiones basadas en evidencia científica.

Cuáles son los tipos más comunes de Estadísticos de Prueba y cuándo se utilizan

En el campo de la estadística, los **estadísticos de prueba** son herramientas fundamentales utilizadas para tomar decisiones basadas en datos y evaluar la evidencia proporcionada por una muestra. Estos estadísticos se calculan a partir de los datos recopilados durante un estudio o experimento y se comparan con valores teóricos o de referencia para determinar si existen diferencias significativas o patrones en los datos.

A continuación, se presentan los tipos más comunes de **estadísticos de prueba**:

1. Estadístico t

El estadístico t es ampliamente utilizado cuando se trabaja con muestras pequeñas (generalmente menos de 30 observaciones). Se utiliza para **probar las diferencias entre las medias de dos grupos independientes** o para **comparar una muestra con una media poblacional conocida**.

2. Estadístico Z

El estadístico Z se aplica cuando se tienen **muestras grandes (más de 30 observaciones)** y su distribución se aproxima a una distribución normal. Es útil para **probar diferencias entre medias o proporciones** y se basa en la **desviación estándar poblacional conocida**.

3. Estadístico Chi-Cuadrado

El estadístico chi-cuadrado es utilizado para **evaluar la relación entre variables categóricas**. Se utiliza específicamente para **probar la independencia o asociación entre dos variables** y se basa en las frecuencias observadas y esperadas en una tabla de contingencia.

4. Estadístico F

El estadístico F se emplea principalmente para **comparar la variabilidad entre dos o más grupos**, utilizando las varianzas. Se utiliza en **análisis de varianza (ANOVA)** y en **pruebas de regresión lineal múltiple**, entre otros.

Estos son solo algunos de los **estadísticos de prueba** más comunes que se utilizan en el análisis de datos. Es importante tener en cuenta que la elección del **estadístico adecuado** dependerá del tipo de datos, el diseño del estudio y las preguntas de investigación planteadas. Además, es fundamental realizar un análisis exhaustivo y tener en cuenta las suposiciones subyacentes al estadístico seleccionado.

Cómo se interpreta el valor del Estadístico de Prueba y qué conclusiones se pueden extraer

La interpretación del valor del Estadístico de Prueba depende en gran medida del tipo de prueba estadística que se esté utilizando y el contexto específico de la investigación. Sin embargo, en general, el valor del Estadístico de Prueba es utilizado para evaluar la evidencia en contra de una hipótesis nula.

Para entender mejor esta interpretación, es importante tener en cuenta dos conceptos clave: el nivel de significancia y el valor p. El nivel de significancia, representado por α (alfa), establece el umbral a partir del cual se considera que el valor del Estadístico de Prueba ofrece suficiente evidencia para rechazar la hipótesis nula. Comúnmente, se utiliza un nivel de significancia de 0.05 o 5%. Esto significa que si el valor p asociado al Estadístico de Prueba es menor a 0.05, se rechaza la hipótesis nula. Si es mayor, no se rechaza.

El valor p, por otro lado, representa la probabilidad de obtener los resultados observados en la muestra, asumiendo que la hipótesis nula es verdadera. Es decir, si el valor p es muy pequeño, indica que los resultados obtenidos serían bastante improbables si la hipótesis nula fuese verdadera, y por lo tanto, se tendría suficiente evidencia para rechazarla. Si el valor p es grande, indicaría que los resultados observados podrían ser comunes incluso bajo la hipótesis nula, y no habría suficiente evidencia para rechazarla.

Es importante tener en cuenta que el valor p no proporciona información sobre la magnitud o relevancia de los resultados, sino únicamente sobre la evidencia en contra de la hipótesis nula. Incluso si se rechaza la hipótesis nula, eso no implica necesariamente que la hipótesis alternativa (la que sostiene el investigador) sea cierta. Solo indica que existen pruebas estadísticas suficientes para cuestionar la hipótesis nula.

Además del nivel de significancia y el valor p, es importante considerar el tamaño de la muestra y el efecto del Estadístico de Prueba. Si bien un valor p menor a 0.05 podría indicar una diferencia estadísticamente significativa, si el tamaño de la muestra es muy grande, es posible que se detecten diferencias pequeñas pero poco relevantes desde el punto de vista práctico.

El valor del Estadístico de Prueba permite evaluar la evidencia en contra de la hipótesis nula y ayuda a tomar decisiones basadas en pruebas estadísticas. Sin embargo, su interpretación debe hacerse teniendo en cuenta el nivel de significancia, el valor p, el tamaño de la muestra y la relevancia práctica de los resultados.

Qué consideraciones se deben tener en cuenta al realizar una prueba de hipótesis con el Estadístico de Prueba

Realizar una prueba de hipótesis con el Estadístico de Prueba implica tener en cuenta varias consideraciones importantes. A continuación, se enumeran algunas de las principales:

1. Definir las hipótesis

Antes de llevar a cabo la prueba de hipótesis, es esencial definir claramente la hipótesis nula y la hipótesis alternativa. La hipótesis nula representa la afirmación que se desea poner a prueba, mientras que la hipótesis alternativa establece la negación de la hipótesis nula.

2. Seleccionar el nivel de significancia

El nivel de significancia indica cuán dispuesto estás a cometer un error de tipo I, es decir, rechazar la hipótesis nula cuando en realidad es verdadera. Es importante elegir un nivel de significancia antes de realizar la prueba de hipótesis, y generalmente se utiliza un nivel estándar como 0.05 (5%) o 0.01 (1%).

3. Determinar la región crítica

La región crítica es el rango de valores del estadístico de prueba para los cuales se rechaza la hipótesis nula. Esto se determina utilizando la distribución de probabilidad adecuada para el estadístico de prueba utilizado en particular, como la distribución t de Student o la distribución chi-cuadrado.

4. Calcular el valor del Estadístico de Prueba

El siguiente paso es calcular el valor del estadístico de prueba utilizando los datos observados en la muestra. Este cálculo depende del tipo de prueba de hipótesis que se esté realizando y de la fórmula correspondiente.

5. Comparar el valor del Estadístico de Prueba con la región crítica

Una vez calculado el valor del estadístico de prueba, se compara con la región crítica previamente determinada. Si el valor del estadístico de prueba se encuentra dentro de la región crítica, se rechaza la hipótesis nula y se acepta la hipótesis alternativa. Si el valor del estadístico de prueba se encuentra fuera de la región crítica, no se tiene evidencia suficiente para rechazar la hipótesis nula.

6. Interpretar los resultados

Finalmente, es importante interpretar los resultados obtenidos. Si la hipótesis nula es rechazada, esto indica que los datos proporcionan evidencia para respaldar la hipótesis alternativa. Por otro lado, si la hipótesis nula no es rechazada, no se puede afirmar concluyentemente la validez de la hipótesis alternativa.

Al realizar una prueba de hipótesis con el Estadístico de Prueba se deben tener en cuenta estas consideraciones importantes, desde definir claramente las hipótesis hasta interpretar correctamente los resultados obtenidos.

Cuál es la importancia de la significancia estadística en relación al Estadístico de Prueba

La significancia estadística es crucial en el campo de la investigación científica, ya que permite determinar si los resultados obtenidos son estadísticamente significativos o simplemente se deben al azar. Para ello, se utiliza una medida llamada Estadístico de Prueba.

El Estadístico de Prueba es un valor numérico que se calcula a partir de los datos recolectados en un estudio y se compara con un umbral crítico establecido previamente. Este umbral representa el nivel de confianza deseado para poder afirmar que los resultados son estadísticamente significativos.

Cómo se calcula el Estadístico de Prueba

El cálculo del Estadístico de Prueba depende del tipo de análisis estadístico que se esté realizando. Por ejemplo, en un análisis de diferencia de medias, se utiliza la fórmula t = (x1 - x2) / sqrt(s12/n1 + s22/n2), donde x1 y x2 son las medias de las dos muestras, s1 y s2 son las desviaciones estándar de las dos muestras, y n1 y n2 son los tamaños de las dos muestras.

Una vez calculado el Estadístico de Prueba, se compara con el valor crítico correspondiente para determinar si los resultados son estadísticamente significativos. Si el Estadístico de Prueba es mayor (o menor, dependiendo del caso) que el valor crítico, se rechaza la hipótesis nula y se concluye que existe una diferencia o relación significativa entre las variables analizadas.

Impacto del Estadístico de Prueba en las investigaciones

El Estadístico de Prueba juega un papel fundamental en las investigaciones científicas, ya que permite obtener conclusiones basadas en evidencia estadística. Al determinar si los resultados son estadísticamente significativos, se asegura que las diferencias o relaciones observadas no son producto del azar.

En caso de que los resultados no sean estadísticamente significativos, esto indica que no hay suficiente evidencia para afirmar la existencia de una diferencia o relación entre las variables. Esto puede ser útil para descartar hipótesis y evitar conclusiones erróneas.

Por otro lado, si los resultados son estadísticamente significativos, se proporciona una base sólida para respaldar teorías o tomar decisiones basadas en esos resultados. Esto tiene un impacto directo en distintos campos, como la medicina, la psicología o la economía, donde se toman decisiones basadas en evidencia científica.

El Estadístico de Prueba es una herramienta clave en la investigación científica, ya que permite determinar si los resultados obtenidos son estadísticamente significativos. Su correcta interpretación y utilización garantiza la validez de los estudios y contribuye al avance del conocimiento en distintas áreas.

Qué alternativas existen al Estadístico de Prueba en la inferencia estadística

El Estadístico de Prueba es una herramienta muy utilizada en el campo de la inferencia estadística para tomar decisiones sobre hipótesis. Sin embargo, existen alternativas a esta técnica que pueden ser igualmente útiles y brindar información adicional sobre los datos.

Análisis Bayesiano

Una de las alternativas más populares al Estadístico de Prueba es el análisis bayesiano. En lugar de realizar inferencias basadas en valores puntuales, el enfoque bayesiano utiliza distribuciones de probabilidad para representar incertidumbre. Este enfoque permite tomar en cuenta información previa y actualizarla a medida que se obtienen nuevos datos, lo cual ofrece resultados más interpretables.

Métodos de resampling

Otra alternativa al Estadístico de Prueba es utilizar métodos de resampling, como el bootstrap o el jackknife. Estos métodos consisten en generar múltiples muestras a partir del conjunto de datos original, y calcular estimaciones y errores a partir de estas muestras. Esto permite obtener intervalos de confianza y estimaciones más precisas que el Estadístico de Prueba tradicional.

Comparación de modelos

En lugar de realizar pruebas de hipótesis, otra alternativa es realizar comparaciones entre modelos. Esta técnica consiste en proponer diferentes modelos que explican los datos y comparar su ajuste utilizando criterios estadísticos, como el criterio de información de Akaike (AIC) o el criterio de información bayesiano (BIC). Estos criterios tienen en cuenta la complejidad del modelo y penalizan aquellos con un ajuste excesivo.

Análisis multivariado

Finalmente, el análisis multivariado también puede ser una alternativa al Estadístico de Prueba. Esta técnica permite estudiar las relaciones entre múltiples variables y puede ser útil en casos donde se desea explorar la interacción entre diversas variables predictoras. Los métodos multivariados, como el análisis de componentes principales o el análisis de correspondencias, pueden revelar patrones y estructuras en los datos que no pueden ser capturados por el Estadístico de Prueba tradicional.

Cómo influye el tamaño de muestra en la determinación del Estadístico de Prueba

El tamaño de muestra es un factor determinante en la estadística y tiene un gran impacto en la determinación del Estadístico de Prueba. El Estadístico de Prueba es una medida utilizada para evaluar la discrepancia entre los datos observados y los valores esperados bajo una hipótesis nula.

Cuando se trata de calcular el Estadístico de Prueba, se utiliza una fórmula que toma en cuenta los valores observados y los valores esperados, así como también el tamaño de muestra. En general, se puede decir que cuanto mayor sea el tamaño de muestra, más precisa será la estimación del Estadístico de Prueba.

Esto se debe a que un mayor tamaño de muestra disminuye la variabilidad de los datos y proporciona una mejor representación de la población total. Por lo tanto, al aumentar el tamaño de muestra, se reduce el margen de error en la estimación del Estadístico de Prueba.

Por otro lado, si el tamaño de muestra es pequeño, existe una mayor posibilidad de obtener resultados sesgados o no representativos de la población. Esto puede afectar la precisión de la estimación del Estadístico de Prueba y, en consecuencia, la validez de los resultados obtenidos.

Es importante tener en cuenta que el tamaño de muestra adecuado depende del tipo de investigación y del fenómeno que se esté estudiando. En general, se recomienda utilizar muestras lo suficientemente grandes como para obtener resultados confiables y representativos, pero no tan grandes como para ser impracticables en términos de tiempo y recursos.

El tamaño de muestra juega un papel crucial en la determinación del Estadístico de Prueba. Un mayor tamaño de muestra proporciona una estimación más precisa del Estadístico de Prueba y reduce el margen de error, mientras que un tamaño de muestra pequeño puede conducir a resultados sesgados o poco representativos.

¿Cuáles son algunos ejemplos prácticos de cómo el Estadístico de Prueba impacta las investigaciones en diferentes campos?

El Estadístico de Prueba es una herramienta fundamental en el análisis estadístico y tiene un impacto significativo en la validez y confiabilidad de los resultados de investigación. A continuación, presentamos algunos ejemplos prácticos de cómo el Estadístico de Prueba puede afectar los hallazgos en diferentes campos:

Análisis de Medicamentos

• En ensayos clínicos para evaluar la eficacia de nuevos medicamentos, el Estadístico de Prueba se utiliza para determinar si existe una diferencia significativa entre el grupo que recibió el medicamento y el grupo de control.
• Si el Estadístico de Prueba muestra una diferencia significativa, se puede concluir que el medicamento en cuestión tiene un efecto positivo en el tratamiento de la enfermedad.
• Por otro lado, si el Estadístico de Prueba no muestra una diferencia significativa, esto indica que el medicamento no es más eficaz que el placebo o el tratamiento convencional.

Análisis de Encuestas

• En investigaciones de opinión pública, el Estadístico de Prueba se utiliza para determinar si las respuestas de diferentes grupos son significativamente diferentes.
• Por ejemplo, en una encuesta sobre la preferencia política, se puede utilizar el Estadístico de Prueba para analizar si hay diferencias significativas entre las respuestas de hombres y mujeres.
• Si el Estadístico de Prueba muestra una diferencia significativa, se pueden extraer conclusiones sobre las preferencias políticas basadas en el género de los encuestados.

Investigación en Ciencias Sociales

• En estudios que analizan fenómenos sociales, el Estadístico de Prueba se utiliza para determinar si hay una relación significativa entre dos variables.
• Por ejemplo, en un estudio sobre el efecto de la educación en los niveles de ingresos, se podría utilizar el Estadístico de Prueba para determinar si existe una diferencia significativa en los ingresos promedio entre personas con diferentes niveles de educación.
• Si el Estadístico de Prueba muestra una diferencia significativa, se puede concluir que la educación tiene un impacto en los niveles de ingresos.

El Estadístico de Prueba es una herramienta esencial en la investigación científica y su uso adecuado garantiza resultados confiables y válidos. Su aplicación en diferentes campos como el análisis de medicamentos, encuestas y ciencias sociales demuestra su relevancia en la generación de conocimiento basado en evidencia.

El Estadístico de Prueba es un valor calculado a partir de los datos de una muestra y se utiliza para tomar decisiones sobre la hipótesis nula en un análisis estadístico.

La interpretación del Estadístico de Prueba depende del tipo de análisis y del contexto de la investigación, pero generalmente se compara con un valor crítico o se calcula un p-valor para determinar si existe evidencia suficiente para rechazar la hipótesis nula.

El Estadístico de Prueba es fundamental en las investigaciones porque nos permite evaluar si los resultados que encontramos son simplemente el producto del azar o si realmente hay una relación o diferencia significativa entre las variables estudiadas.

El cálculo del Estadístico de Prueba varía dependiendo del tipo de análisis estadístico utilizado, pero generalmente se basa en comparar diferencias entre los datos observados y los datos esperados bajo la hipótesis nula, aplicando fórmulas específicas para cada tipo de prueba.

Si el Estadístico de Prueba no es significativo, significa que no hay suficiente evidencia para rechazar la hipótesis nula y se concluye que los resultados son consistentes con lo esperado bajo dicha hipótesis.