Desentraña el fascinante mundo del movimiento en dos dimensiones: ¡Descubre cómo funciona y sorpréndete con sus aplicaciones!
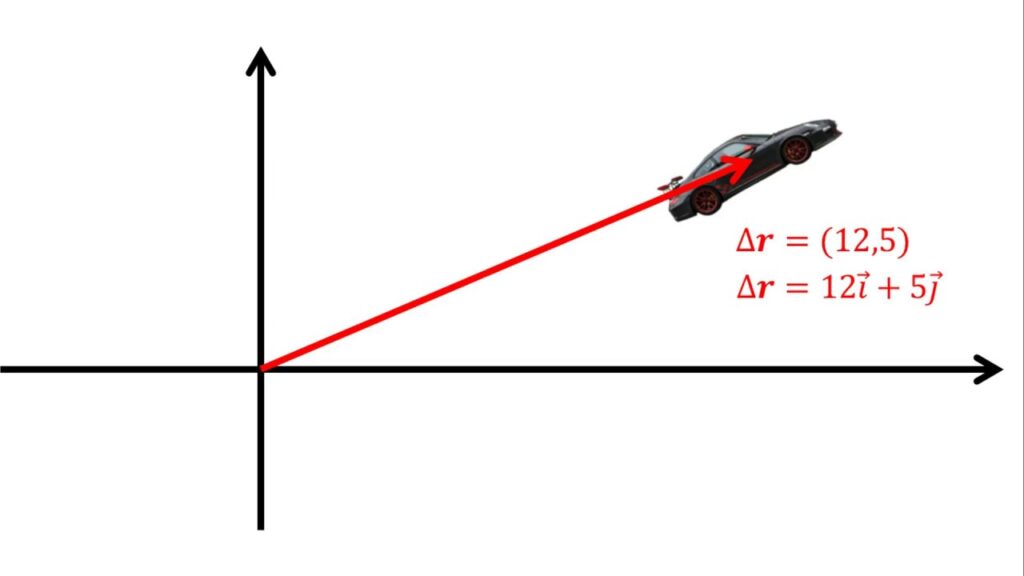
El movimiento en dos dimensiones es un concepto fundamental en la física que nos permite entender cómo se desplazan los objetos en el espacio. A diferencia del movimiento en una dimensión, donde solo se analiza un eje, el movimiento en dos dimensiones implica considerar tanto la posición como la velocidad en dos direcciones perpendiculares entre sí.
Exploraremos en detalle cómo funciona el movimiento en dos dimensiones y sus principales características. Analizaremos los vectores de posición y velocidad, así como las leyes fundamentales que rigen el movimiento, como la conservación de la energía y el momento lineal. También examinaremos algunas aplicaciones prácticas del movimiento en dos dimensiones, como el lanzamiento de proyectiles y la dinámica de sistemas de partículas. ¡Prepárate para adentrarte en un fascinante mundo de trayectorias y colisiones!
Qué es el movimiento en dos dimensiones y cómo funciona
El movimiento en dos dimensiones es aquel que se produce en un plano que consta de dos ejes perpendiculares: el eje x o horizontal y el eje y o vertical. Esta forma de movimiento se encuentra presente en muchas situaciones de la vida cotidiana, como el lanzamiento de un objeto al aire, el desplazamiento de un coche por una carretera recta o incluso el vuelo de un pájaro.
Para comprender cómo funciona el movimiento en dos dimensiones, es importante entender los conceptos de velocidad y aceleración. La velocidad se define como la relación entre el cambio de posición de un objeto en un determinado tiempo. En el caso del movimiento en dos dimensiones, la velocidad tiene dos componentes: la velocidad en el eje x y la velocidad en el eje y.
Por otro lado, la aceleración se refiere al cambio en la velocidad de un objeto en un determinado tiempo. Al igual que la velocidad, la aceleración también tiene componentes en ambos ejes. Estas dos componentes permiten describir el cambio de dirección y magnitud del movimiento en dos dimensiones.
En cuanto a las leyes fundamentales que rigen el movimiento en dos dimensiones, podemos mencionar la primera ley de Newton o ley de inercia, que establece que un objeto en reposo permanecerá en reposo y un objeto en movimiento continuará moviéndose a una velocidad constante en línea recta a menos que una fuerza externa actúe sobre él.
Otra ley importante es la segunda ley de Newton, que establece que la aceleración de un objeto es directamente proporcional a la fuerza neta que actúa sobre él e inversamente proporcional a su masa. Esto se expresa mediante la famosa fórmula F = m * a, donde F representa la fuerza neta, m es la masa del objeto y a es la aceleración.
Además de estas leyes fundamentales, existen diferentes ecuaciones que permiten calcular el movimiento en dos dimensiones, como las ecuaciones de posición, velocidad y aceleración. Estas ecuaciones se utilizan para determinar la trayectoria, velocidad final o posición final de un objeto en función del tiempo transcurrido y las condiciones iniciales.
El movimiento en dos dimensiones es aquel que se produce en un plano con ejes x e y, y se rige por las leyes de Newton, así como diversas ecuaciones que nos permiten describir y calcular su comportamiento. Su comprensión es fundamental en disciplinas como la física y la ingeniería, y tiene una amplia variedad de aplicaciones en campos como la navegación, la construcción de puentes, el diseño de videojuegos y muchas otras áreas.
Cuáles son las leyes físicas que rigen el movimiento en dos dimensiones
El movimiento en dos dimensiones es gobernado por las mismas leyes físicas que rigen el movimiento en una dimensión, pero con algunas diferencias clave. En lugar de considerar solo la posición y la velocidad en una línea recta, debemos tener en cuenta tanto la posición como la velocidad en dos direcciones diferentes: horizontal y vertical.
La ley fundamental que describe el movimiento en dos dimensiones es la segunda ley de Newton, que establece que la aceleración experimentada por un objeto es igual a la fuerza neta aplicada sobre él dividida por su masa. Esta ley se puede expresar matemáticamente como:
F = m * a
Donde F es la fuerza neta, m es la masa del objeto y a es su aceleración.
Para aplicar esta ley al movimiento en dos dimensiones, debemos descomponer la fuerza y la aceleración en sus componentes horizontal y vertical. Por ejemplo, si un objeto se mueve en un plano inclinado, podemos descomponer la fuerza neta en una componente paralela al plano (horizontal) y otra componente perpendicular al plano (vertical).
Otra ley importante para entender el movimiento en dos dimensiones es la ley de conservación del momento lineal. Esta ley establece que, en ausencia de fuerzas externas, la cantidad total de momento lineal de un sistema cerrado se conserva. Matemáticamente, se expresa como:
p = m * v
Donde p representa el momento lineal, m es la masa del objeto y v es su velocidad.
En el caso del movimiento en dos dimensiones, debemos tener en cuenta tanto la magnitud como la dirección del momento lineal en cada una de las direcciones.
Ejemplos de aplicaciones del movimiento en dos dimensiones
Continúa escribiendo el contenido para esa sección.
Cómo se puede representar el movimiento en dos dimensiones con ecuaciones
El movimiento en dos dimensiones se puede representar utilizando ecuaciones que describen la posición, velocidad y aceleración de un objeto en un plano cartesiano. Estas ecuaciones son fundamentales para comprender y predecir el movimiento de objetos en situaciones donde intervienen dos direcciones diferentes.
Ecuación de posición en dos dimensiones
La ecuación de posición en dos dimensiones nos permite determinar la ubicación de un objeto en un sistema de coordenadas cartesianas. Se expresa mediante las coordenadas (x, y) del objeto en un instante dado t:
x = x0 + v0xt + 1/2axt^2
y = y0 + v0yt + 1/2ayt^2
Donde:
xyyson las coordenadas del objeto en el instante t.x0yy0son las coordenadas iniciales del objeto.v0xyv0yson las componentes iniciales de la velocidad.axyayson las componentes de la aceleración.tes el tiempo transcurrido.
Esta ecuación nos permite calcular la posición exacta de un objeto en función del tiempo y su movimiento en las direcciones x e y.
Ecuación de velocidad en dos dimensiones
La ecuación de velocidad en dos dimensiones nos permite determinar la velocidad de un objeto en un instante dado t. Se expresa mediante las componentes (vx, vy) del vector velocidad:
vx = v0x + axt
vy = v0y + ayt
Donde:
vxyvyson las componentes de la velocidad en el instante t.v0xyv0yson las componentes iniciales de la velocidad.axyayson las componentes de la aceleración.tes el tiempo transcurrido.
Estas ecuaciones nos permiten calcular la velocidad de un objeto en función del tiempo y su aceleración en ambas direcciones.
Ecuación de aceleración en dos dimensiones
La ecuación de aceleración en dos dimensiones nos permite determinar la aceleración de un objeto en un instante dado t. Se expresa mediante las componentes (ax, ay) del vector aceleración:
ax = Δvx / t
ay = Δvy / t
Donde:
axyayson las componentes de la aceleración en el instante t.ΔvxyΔvyson los cambios en las componentes de la velocidad.tes el tiempo transcurrido.
Estas ecuaciones nos permiten determinar la aceleración de un objeto en función de los cambios en sus velocidades en ambas direcciones y el tiempo transcurrido.
Cuál es la diferencia entre velocidad y aceleración en el movimiento en dos dimensiones
En el movimiento en dos dimensiones, es importante comprender la diferencia entre velocidad y aceleración. Si bien ambos términos están relacionados con el cambio de posición de un objeto en el tiempo, cada uno describe una propiedad diferente del movimiento.
Velocidad
La velocidad en el movimiento en dos dimensiones se refiere a la tasa de cambio de la posición de un objeto en relación con el tiempo. En otras palabras, la velocidad nos dice qué tan rápido se desplaza un objeto y en qué dirección. Se expresa como una magnitud (la rapidez) seguida de una dirección (por ejemplo, hacia arriba, hacia abajo, hacia la derecha, hacia la izquierda).
La velocidad puede ser constante o cambiar con el tiempo. Cuando la velocidad es constante, decimos que el objeto se mueve a una velocidad uniforme. Esto significa que el objeto recorre distancias iguales en intervalos de tiempo iguales.
La fórmula para calcular la velocidad media en dos dimensiones es:
V = ΔS / Δt
Donde V es la velocidad media, ΔS es el cambio en la posición del objeto y Δt es el cambio en el tiempo.
Aceleración
Por otro lado, la aceleración en el movimiento en dos dimensiones se refiere al cambio en la velocidad de un objeto en relación con el tiempo. La aceleración puede ser positiva (aumentando la velocidad) o negativa (disminuyendo la velocidad). Al igual que la velocidad, la aceleración también tiene magnitud y dirección.
La aceleración no solo se refiere a cambios en la rapidez, sino también a cambios en la dirección del movimiento. Por ejemplo, si un objeto se mueve en línea recta y luego cambia repentinamente de dirección, experimentará una aceleración debido al cambio en su velocidad y dirección.
La fórmula para calcular la aceleración media en dos dimensiones es:
A = ΔV / Δt
Donde A es la aceleración media, ΔV es el cambio en la velocidad del objeto y Δt es el cambio en el tiempo.
Mientras que la velocidad se refiere a qué tan rápido se desplaza un objeto en cierta dirección, la aceleración se refiere a cómo cambia la velocidad de ese objeto en relación con el tiempo. Ambos conceptos son fundamentales para comprender y describir el movimiento en dos dimensiones.
Cuáles son las principales aplicaciones del movimiento en dos dimensiones en la vida cotidiana
El movimiento en dos dimensiones es una parte fundamental de nuestra vida cotidiana, y tiene una amplia variedad de aplicaciones en diferentes campos. A continuación, se presentan algunas de las principales aplicaciones del movimiento en dos dimensiones:
1. Transporte
Una de las aplicaciones más evidentes del movimiento en dos dimensiones es el transporte. Desde automóviles hasta trenes y aviones, todos estos medios de transporte utilizan principios de física y movimiento en dos dimensiones para desplazarse de un lugar a otro. Además, los sistemas de navegación por satélite también hacen uso de cálculos de movimiento en dos dimensiones para determinar la posición y el tiempo de llegada.
2. Deportes y juegos
Los deportes y los juegos también hacen uso del movimiento en dos dimensiones. Por ejemplo, en deportes como el fútbol o el baloncesto, los jugadores deben calcular la trayectoria y velocidad de un balón para lograr marcar un gol o realizar un tiro exitoso. Los videojuegos también utilizan cálculos de movimiento en dos dimensiones para simular el movimiento realista de personajes y objetos en el juego.
3. Diseño de parques temáticos
El diseño y construcción de parques temáticos también hacen uso del movimiento en dos dimensiones para crear atracciones emocionantes. Las montañas rusas, por ejemplo, se basan en los principios del movimiento en dos dimensiones para proporcionar sensaciones extremas a los pasajeros. Los ingenieros y diseñadores utilizan cálculos precisos para determinar las fuerzas y velocidades necesarias para que la montaña rusa proporcione una experiencia segura pero emocionante.
4. Cine y animación
En la industria del cine y la animación, el movimiento en dos dimensiones es crucial. Desde películas animadas hasta efectos especiales en películas de acción, se utilizan técnicas de movimiento en dos dimensiones para crear escenas dinámicas y realistas. Las películas de animación hacen uso de cálculos precisos de movimiento en dos dimensiones para dar vida a personajes y objetos virtuales, mientras que los efectos especiales utilizan esta tecnología para simular movimientos y colisiones impresionantes.
5. Ingeniería y arquitectura
En los campos de la ingeniería y la arquitectura, el movimiento en dos dimensiones también desempeña un papel importante. Los ingenieros estructurales, por ejemplo, deben considerar el movimiento en dos dimensiones al diseñar puentes, edificios y otros proyectos de construcción para garantizar su estabilidad y resistencia ante diferentes fuerzas. Del mismo modo, los arquitectos utilizan principios de movimiento en dos dimensiones para calcular la distribución del espacio y la forma de los edificios.
Estas son solo algunas de las aplicaciones más comunes del movimiento en dos dimensiones en nuestra vida cotidiana. Es fascinante ver cómo estos conceptos teóricos de la física se aplican en tantos aspectos prácticos de nuestro mundo.
Cómo se utiliza el movimiento en dos dimensiones en la industria de los videojuegos
El movimiento en dos dimensiones es fundamental en la industria de los videojuegos, ya que permite crear mundos virtuales llenos de acción y aventura. A través de técnicas de programación y diseño, se logra simular el movimiento de personajes, objetos y escenarios en un plano bidimensional.
Una de las formas más comunes de utilizar el movimiento en dos dimensiones en los videojuegos es a través de los sprites. Los sprites son imágenes o animaciones que representan a los diferentes elementos del juego, como los personajes, enemigos, objetos y fondos. Mediante la técnica de animación por frames, se van mostrando sucesivamente los diferentes cuadros de la animación, creando así la ilusión de movimiento.
Además del uso de los sprites, también se utiliza la física para simular el movimiento de los objetos en el juego. A través de fórmulas matemáticas y algoritmos, se calcula la velocidad, aceleración y dirección de los elementos del juego, permitiendo así que interactúen entre sí y se muevan de manera realista.
Aplicaciones del movimiento en dos dimensiones en los videojuegos
- Plataformas: En los juegos de plataformas, el movimiento en dos dimensiones cobra especial relevancia. Permite al jugador controlar al personaje principal para que salte, corra y evite obstáculos mientras avanza por los diferentes niveles del juego.
- Disparos: En los juegos de disparos, el movimiento en dos dimensiones se utiliza para simular el movimiento de balas, proyectiles y explosiones. Esto añade emoción y desafío al juego, ya que el jugador debe calcular la trayectoria de los disparos y evitar ser alcanzado por sus enemigos.
- Combates: Los juegos de lucha también hacen uso del movimiento en dos dimensiones para crear coreografías de combate impresionantes. Los movimientos de puñetazos, patadas y bloqueos se representan a través de animaciones que brindan una experiencia visualmente impactante y dinámica al jugador.
- Racing: En los juegos de carreras, el movimiento en dos dimensiones es clave para simular la velocidad y la competencia. Se utiliza para representar la posición y el movimiento de los vehículos en la pista, así como también para crear efectos visuales de derrapes, choques y aceleraciones.
El movimiento en dos dimensiones es un elemento esencial en la industria de los videojuegos. No solo permite crear mundos virtuales llenos de acción y aventura, sino que también añade desafío, emoción y realismo a la experiencia de juego. A través de técnicas de programación y diseño, se logra simular el movimiento de personajes, objetos y escenarios, proporcionando así una diversión única y cautivadora para los jugadores.
¿Qué impacto tiene el movimiento en dos dimensiones en la cinematografía y animación?
El movimiento en dos dimensiones ha tenido un impacto significativo en el campo de la cinematografía y la animación. Permíteme explicarte cómo funciona este fascinante concepto y cómo ha revolucionado estas industrias.
Movimiento en dos dimensiones: una introducción
Antes de sumergirnos en las aplicaciones del movimiento en dos dimensiones, es importante entender qué significa exactamente este concepto. En esencia, el movimiento en dos dimensiones se refiere a la representación visual del movimiento en un plano bidimensional, como una pantalla o una hoja de papel.
En el cine y la animación, el movimiento en dos dimensiones se logra creando una serie de imágenes estáticas que se reproducen rápida y continuamente, dando la ilusión de movimiento. Estas imágenes, conocidas como fotogramas, capturan las diferentes posiciones del sujeto en movimiento en momentos específicos en el tiempo.
Esta técnica se basa en la persistencia de la visión, un fenómeno óptico en el cual nuestra retina retiene brevemente una imagen después de que desaparezca de nuestra vista. Al mostrar rápidamente una secuencia de imágenes, nuestro cerebro interpreta esto como movimiento continuo.
Aplicaciones en la cinematografía
El movimiento en dos dimensiones ha sido fundamental en la historia y evolución del cine. Desde las primeras películas mudas hasta la era moderna del cine digital, esta técnica ha permitido contar historias de manera más dinámica y cautivadora.
La posibilidad de crear movimientos fluidos y realistas en la pantalla ha abierto un mundo de posibilidades en términos de narración visual. Los directores y cineastas han utilizado el movimiento en dos dimensiones para crear momentos de acción emocionantes, secuencias de baile elaboradas e incluso para representar situaciones surrealistas.
Además, esta técnica ha permitido la combinación de imágenes reales con elementos generados por computadora, dando como resultado efectos visuales asombrosos y mundos completamente nuevos.
Aplicaciones en la animación
En el campo de la animación, el movimiento en dos dimensiones es esencial. Desde los primeros dibujos animados hasta las últimas producciones animadas por computadora, esta técnica ha sido utilizada para dar vida a personajes y contar historias coloridas y envolventes.
La animación tradicional, también conocida como animación a mano alzada, sigue siendo apreciada por su belleza artística y su capacidad para transmitir emociones. A través del uso de fotogramas, los animadores pueden crear movimientos fluidos y expresivos, permitiendo que los personajes cobren vida en la pantalla.
Además, el movimiento en dos dimensiones también ha abierto puertas a nuevas formas de animación, como la animación de recortes y la animación digital. Estas técnicas han llevado la animación a un nivel aún más creativo y han ampliado las posibilidades de diseño visual.
El movimiento en dos dimensiones es un concepto fundamental tanto en el cine como en la animación. Gracias a esta técnica, podemos disfrutar de películas y animaciones que nos transportan a distintos mundos e historias.
¿Cuáles son los desafíos y problemas comunes asociados al estudio del movimiento en dos dimensiones?
El estudio del movimiento en dos dimensiones presenta diversos desafíos y problemas que los científicos e ingenieros deben abordar. A continuación, se presentan algunos de los más comunes:
Fricción
La fricción es una fuerza resistente que actúa sobre un objeto cuando este se desplaza sobre una superficie. En el caso del movimiento en dos dimensiones, la fricción puede afectar tanto el desplazamiento horizontal como el vertical. Comprender cómo la fricción influye en el movimiento y cómo calcularla correctamente es fundamental para el análisis y diseño de sistemas que interactúen con esta fuerza.
Resistencia del aire
Cuando un objeto se mueve a través del aire, experimenta una resistencia opuesta a su movimiento conocida como resistencia del aire. Esta fuerza puede ser significativa, especialmente a altas velocidades o en objetos con una gran área superficial. La resistencia del aire puede dificultar la predicción precisa del movimiento en dos dimensiones y debe tenerse en cuenta al diseñar estructuras o vehículos que interactúen con el aire.
Aceleración gravitacional
En el movimiento en dos dimensiones, la aceleración gravitacional juega un papel importante en el desplazamiento vertical de un objeto. Aunque en muchos casos se supone que la aceleración gravitacional es constante (9.8 m/s²), existen situaciones en las que puede variar, lo cual añade complejidad al estudio del movimiento en dos dimensiones.
Movimientos complejos
Los movimientos en dos dimensiones pueden volverse considerablemente más complejos cuando hay múltiples fuerzas actuando sobre un objeto o cuando se presentan situaciones en las que la dirección y magnitud de estas fuerzas cambian en el tiempo. En estos casos, es necesario emplear métodos avanzados de análisis matemático y físico para poder comprender y predecir adecuadamente el comportamiento del movimiento en dos dimensiones.
Dinámica de colisiones
Las colisiones entre objetos en movimiento son eventos comunes y tienen una gran relevancia en diversas áreas, desde la física hasta la ingeniería. Estudiar y comprender cómo se producen las colisiones en dos dimensiones implica analizar la conservación de la energía y del momento lineal, así como considerar factores como la elasticidad de los objetos involucrados. Es importante tener en cuenta estos aspectos al diseñar sistemas que interactúen con colisiones en dos dimensiones.
Estos son solo algunos de los desafíos y problemas comunes asociados al estudio del movimiento en dos dimensiones. A pesar de su complejidad, el movimiento en dos dimensiones tiene aplicaciones fascinantes en campos como la física, la ingeniería estructural y mecánica, la biología del movimiento y la animación por computadora, lo cual hace que su comprensión sea esencial para el avance de estas disciplinas.
Cómo se pueden resolver los problemas de movimiento en dos dimensiones utilizando herramientas matemáticas y físicas
El movimiento en dos dimensiones es un concepto fundamental en la física y tiene una amplia gama de aplicaciones prácticas. Para entender cómo funciona y resolver problemas relacionados con el movimiento en dos dimensiones, podemos utilizar herramientas matemáticas y físicas.
Herramientas matemáticas para el estudio del movimiento en dos dimensiones
La matemática proporciona las herramientas necesarias para describir y analizar el movimiento en dos dimensiones con precisión. Una de las herramientas más utilizadas es el sistema de coordenadas cartesianas, que nos permite representar la posición de un objeto en el plano utilizando dos ejes perpendiculares entre sí.
Además, podemos utilizar ecuaciones matemáticas para describir el movimiento en dos dimensiones. Por ejemplo, la ecuación de la trayectoria nos permite determinar la posición de un objeto en función del tiempo a lo largo de su movimiento. También podemos utilizar la ecuación de velocidad para determinar la velocidad de un objeto en cualquier punto de su trayectoria.
Otra herramienta matemática importante para el estudio del movimiento en dos dimensiones es el cálculo diferencial e integral. Estas ramas de las matemáticas nos permiten calcular la derivada y la integral de una función, lo cual es útil para determinar la velocidad y la aceleración de un objeto en movimiento.
Herramientas físicas para el estudio del movimiento en dos dimensiones
Además de las herramientas matemáticas, la física ofrece conceptos y leyes fundamentales que nos ayudan a comprender y analizar el movimiento en dos dimensiones. La cinemática es una rama de la física que se dedica al estudio del movimiento de los cuerpos sin tener en cuenta las causas que lo producen.
La primera ley del movimiento de Newton, también conocida como la ley de inercia, establece que un objeto en reposo permanecerá en reposo y un objeto en movimiento continuará moviéndose con velocidad constante en línea recta, a menos que una fuerza externa actúe sobre él. Esta ley es fundamental para comprender el movimiento en dos dimensiones, ya que nos permite predecir cómo se comportará un objeto sin tener en cuenta las fuerzas externas que actúan sobre él.
Por otro lado, la segunda ley del movimiento de Newton establece que la aceleración de un objeto es directamente proporcional a la fuerza neta que actúa sobre él e inversamente proporcional a su masa. Esta ley nos permite relacionar la fuerza neta aplicada a un objeto con la aceleración que adquiere.
Otra ley importante para el estudio del movimiento en dos dimensiones es la ley de conservación de la cantidad de movimiento. Esta ley establece que, en ausencia de fuerzas externas, la cantidad total de momento lineal de un sistema aislado se conserva. Esto significa que si no hay fuerzas externas actuando sobre un sistema de objetos en movimiento, la suma de los momentos lineales antes y después del evento se mantendrá constante.
Estas herramientas físicas nos permiten analizar y resolver problemas de movimiento en dos dimensiones de manera precisa y rigurosa.
Preguntas frecuentes (FAQ)
1. ¿Qué es el movimiento en dos dimensiones?
El movimiento en dos dimensiones es aquel en el cual los objetos se desplazan tanto horizontalmente como verticalmente.
2. ¿Cuál es la fórmula para calcular la velocidad en dos dimensiones?
La fórmula para calcular la velocidad en dos dimensiones es v = √(vx² + vy²), donde vx representa la velocidad en el eje x y vy representa la velocidad en el eje y.
3. ¿Cuál es la diferencia entre el movimiento rectilíneo y el movimiento curvilíneo en dos dimensiones?
En el movimiento rectilíneo, los objetos se desplazan en línea recta, mientras que en el movimiento curvilíneo, los objetos siguen una trayectoria curva.
4. ¿Cuál es la aceleración promedio en dos dimensiones?
La aceleración promedio en dos dimensiones se calcula utilizando la fórmula a = (vf - vi) / t, donde vf es la velocidad final, vi es la velocidad inicial y t es el tiempo transcurrido.
5. ¿Cuáles son algunas aplicaciones del movimiento en dos dimensiones?
Algunas aplicaciones del movimiento en dos dimensiones incluyen el estudio de proyectiles, el análisis de movimientos de objetos en caída libre y la simulación de movimientos en videojuegos.
Deja una respuesta
Entradas relacionadas