El fascinante origen del Teorema de Pitágoras: descubre quién lo inventó y cómo cambiará tu perspectiva sobre las matemáticas

El Teorema de Pitágoras es uno de los principales conceptos en la geometría y las matemáticas, y ha fascinado a generaciones de estudiantes y profesionales del campo. Este teorema establece una relación fundamental entre los lados de un triángulo rectángulo y ha sido utilizado durante siglos para resolver problemas relacionados con la medida de distancias y áreas.

Exploraremos el origen del Teorema de Pitágoras y cómo fue descubierto por los antiguos matemáticos griegos. También discutiremos cómo este teorema cambió radicalmente la forma en que se entendían las matemáticas en su tiempo e incluso hasta el día de hoy. Si alguna vez te has preguntado quién inventó esta regla tan importante o qué aplicaciones prácticas tiene en la vida cotidiana, sigue leyendo para descubrirlo todo.

De dónde proviene el Teorema de Pitágoras

El Teorema de Pitágoras es uno de los conceptos más conocidos y utilizados en las matemáticas. Este teorema establece una relación entre los lados de un triángulo rectángulo y ha sido utilizado durante siglos para resolver problemas geométricos y aplicaciones prácticas.

Aunque el teorema lleva el nombre de Pitágoras, no fue necesariamente él quien lo inventó. El origen exacto del Teorema de Pitágoras es desconocido y se ha debatido durante muchos años.

No obstante, algunos historiadores sugieren que el teorema puede haber sido conocido mucho antes de la época de Pitágoras. Por ejemplo, en las antiguas civilizaciones de Mesopotamia y Egipto había evidencia de que ya se utilizaban triples de números enteros que cumplían con la relación del teorema.

Sin embargo, se atribuye a Pitágoras y su escuela en el siglo VI a.C. la formulación y demostración formal del teorema. Aunque no hay evidencia escrita directa de esto, se cree que los pitagóricos utilizaron su comprensión de las proporciones, los números irracionales y la geometría para mostrar que, en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados.

La influencia de los pitagóricos y su teorema fue enorme en la historia de las matemáticas. Su enfoque en la importancia de las relaciones numéricas y geométricas sentó las bases para el desarrollo posterior de la geometría euclidiana y otras ramas de las matemáticas.

Aplicaciones prácticas del Teorema de Pitágoras

A lo largo de los siglos, el Teorema de Pitágoras ha sido utilizado para resolver una amplia variedad de problemas prácticos en diversas áreas, como la arquitectura, la navegación y la física. Su utilidad radica en que permite calcular la longitud de un lado desconocido de un triángulo rectángulo si se conocen las longitudes de los otros dos lados.

Por ejemplo, en arquitectura, se puede utilizar el teorema para asegurar que una estructura sea estable o para determinar las dimensiones necesarias de un objeto. En navegación, el teorema es fundamental para calcular distancias y ángulos en mapas o para determinar la altura de un faro desde un barco.

Incluso en la vida cotidiana, el Teorema de Pitágoras puede ser útil. Por ejemplo, si queremos medir directamente la distancia en línea recta entre dos puntos, podemos aplicar el teorema para calcularla sin tener que recorrer todo el camino.

El Teorema de Pitágoras es un concepto matemático fascinante y versátil que ha influido en el desarrollo de las matemáticas a lo largo de la historia. Aunque su origen exacto sigue siendo un misterio, su aplicación práctica y su importancia en diversos campos demuestran su relevancia en nuestro mundo.

Quién fue el inventor del Teorema de Pitágoras

El Teorema de Pitágoras, uno de los conceptos matemáticos más conocidos y utilizados en todo el mundo, no fue realmente inventado por una sola persona. Su origen se remonta a la antigua civilización griega, pero varios matemáticos contribuyeron a su desarrollo y comprensión a lo largo de los años.

Uno de los primeros indicios del teorema se encuentra en una tabla babilónica de arcilla del siglo XVIII a.C., conocida como Plimpton 322. Esta tabla muestra una lista de tripletes pitagóricos, es decir, conjuntos de números enteros que cumplen con la ecuación a^2 + b^2 = c^2. Sin embargo, no se sabe si los babilonios realmente comprendían la importancia o el significado del teorema en sí.

Fue el filósofo y matemático griego Pitágoras de Samos quien llevó el teorema a un nivel más profundo de comprensión. Pitágoras y sus seguidores, conocidos como los pitagóricos, estudiaron las propiedades de los números enteros y descubrieron que las relaciones entre los lados de los triángulos rectángulos seguían un patrón específico. Aunque no se le atribuye el descubrimiento directo del teorema, Pitágoras y su escuela fueron los que le dieron nombre y establecieron los fundamentos para su demostración y aplicación.

Además de Pitágoras, otros matemáticos antiguos también hicieron importantes contribuciones al desarrollo del teorema. Entre ellos se encuentran Euclides, quien demostró el teorema de manera axiomática en su famoso libro "Elementos", y Arquímedes, quien utilizó el teorema para calcular áreas y volúmenes en sus trabajos sobre geometría.

A lo largo de la historia, muchos otros matemáticos y científicos han estudiado el teorema y han aportado nuevas ideas y demostraciones. Algunos nombres destacados incluyen a Leonardo da Vinci, René Descartes, Isaac Newton y Carl Friedrich Gauss, entre otros.

Aunque no se puede atribuir el descubrimiento del Teorema de Pitágoras a una sola persona, fue Pitágoras y su escuela quienes contribuyeron significativamente a su desarrollo e investigación. Su legado ha dejado una huella perdurable en el campo de las matemáticas y ha cambiado nuestra perspectiva sobre las relaciones numéricas y geométricas en el mundo que nos rodea.

Cuál es la importancia del Teorema de Pitágoras en las matemáticas

El Teorema de Pitágoras es uno de los conceptos matemáticos más importantes y fundamentales en la geometría euclidiana. Este teorema establece una relación fundamental entre los lados de un triángulo rectángulo, lo cual ha tenido amplias implicaciones en diversas ramas de las matemáticas y en campos como la física, la arquitectura y la ingeniería.

En términos sencillos, el teorema establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de las longitudes de los otros dos lados, conocidos como catetos. Matemáticamente se expresa de la siguiente manera:

c^2 = a^2 + b^2

Donde c representa la hipotenusa y a y b representan los catetos del triángulo rectángulo.

La importancia de este teorema radica en que proporciona una relación precisa y predecible entre los elementos de un triángulo rectángulo, permitiendo su resolución sin necesidad de mediciones exactas. Esto ha sido fundamental para el desarrollo de la geometría y la trigonometría, así como para el estudio de otras áreas de las matemáticas.

Además, el Teorema de Pitágoras también ha sido utilizado ampliamente en aplicaciones prácticas en la vida cotidiana. Desde el diseño de edificios y la construcción de puentes hasta la navegación marítima y los avances tecnológicos, este teorema ha sido una herramienta invaluable para los científicos y los ingenieros.

El Teorema de Pitágoras es un concepto matemático clave que ha revolucionado nuestra comprensión de la geometría y ha tenido amplias aplicaciones en diversas ramas de las matemáticas y en el mundo real. Su importancia radica en su capacidad para proporcionar una relación precisa y predecible entre los elementos de un triángulo rectángulo, lo cual ha llevado a numerosos descubrimientos y avances en la historia de las matemáticas.

Cómo funciona el Teorema de Pitágoras

El Teorema de Pitágoras es una de las herramientas fundamentales en la geometría. Establece una relación matemática entre los lados de un triángulo rectángulo, es decir, aquel que tiene un ángulo recto de 90 grados.

El teorema establece lo siguiente: "En todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos". La hipotenusa es el lado más largo de un triángulo rectángulo y se representa con la letra "c", mientras que los catetos son los otros dos lados y se representan con las letras "a" y "b".

Matemáticamente, esto se puede expresar de la siguiente manera:

c² = a² + b²

Para entender mejor esto, imaginemos un triángulo rectángulo con una hipotenusa de longitud 5 y un cateto de longitud 3. Según el teorema de Pitágoras, podemos encontrar la longitud del otro cateto utilizando esta fórmula:

c² = a² + b²
5² = 3² + b²
25 = 9 + b²
b² = 25 - 9 = 16
b = √16 = 4

Por lo tanto, la longitud del otro cateto sería 4. Este es solo un ejemplo sencillo, pero el teorema de Pitágoras se puede aplicar en diferentes contextos y para resolver problemas más complejos en geometría.

Es importante destacar que el Teorema de Pitágoras solo se aplica a triángulos rectángulos, y no a otro tipo de triángulos. Además, este teorema tiene diversas aplicaciones prácticas en la vida cotidiana, como en la arquitectura, navegación, astronomía, entre otras disciplinas.

Cuál es la fórmula del Teorema de Pitágoras

La fórmula del Teorema de Pitágoras es una de las más conocidas y utilizadas en matemáticas. Esta fórmula establece la relación entre los lados de un triángulo rectángulo, es decir, un triángulo que posee un ángulo recto (90 grados).

La fórmula se expresa de la siguiente manera:

a2 + b2 = c2

Donde "c" representa la hipotenusa del triángulo rectángulo, y "a" y "b" representan los catetos. El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Ejemplo práctico:

Supongamos que tenemos un triángulo rectángulo con catetos de medida 3 unidades cada uno. Si queremos conocer la medida de la hipotenusa, podemos utilizar el Teorema de Pitágoras.

Sustituyendo los valores en la fórmula, obtendríamos lo siguiente:

32 + 32 = c2

Realizando las operaciones, tendríamos:

9 + 9 = c2

Finalmente, sumando los valores, obtenemos:

18 = c2

Para despejar "c", la hipotenusa, simplemente necesitamos calcular la raíz cuadrada de ambos lados:

c = √18

La hipotenusa del triángulo rectángulo correspondiente tiene una medida aproximada de 4.24 unidades.

Esta es la fórmula básica del Teorema de Pitágoras y su aplicación práctica para resolver problemas geométricos que involucren triángulos rectángulos.

Cómo se aplica el Teorema de Pitágoras en problemas prácticos

El Teorema de Pitágoras es una herramienta fundamental en matemáticas, que permite calcular la longitud desconocida de un lado de un triángulo rectángulo. Aunque su formulación matemática puede parecer compleja, su aplicación en problemas prácticos es bastante sencilla y versátil.

Cálculo de la hipotenusa

Una de las aplicaciones más comunes del Teorema de Pitágoras es el cálculo de la hipotenusa de un triángulo rectángulo cuando se conocen los valores de sus dos catetos. Para ello, simplemente debemos sustituir los valores de los catetos en la fórmula del teorema y realizar la operación correspondiente.

c^2 = a^2 + b^2

Donde "c" representa la hipotenusa y "a" y "b" son los catetos conocidos. Aplicando esta fórmula, obtenemos el valor de la hipotenusa, que nos permitirá conocer la longitud total del triángulo rectángulo.

Cálculo de un cateto

Además de calcular la hipotenusa, el Teorema de Pitágoras también se puede utilizar para determinar el valor de uno de los catetos de un triángulo rectángulo, siempre y cuando se conozcan el valor de la hipotenusa y otro cateto.

a^2 = c^2 - b^2

b^2 = c^2 - a^2

Estas fórmulas nos permiten despejar el valor del cateto conocido, utilizando los valores de la hipotenusa y el otro cateto. Al sustituir en la fórmula correspondiente y realizar las operaciones, obtendremos el valor del cateto desconocido.

Cálculo de áreas

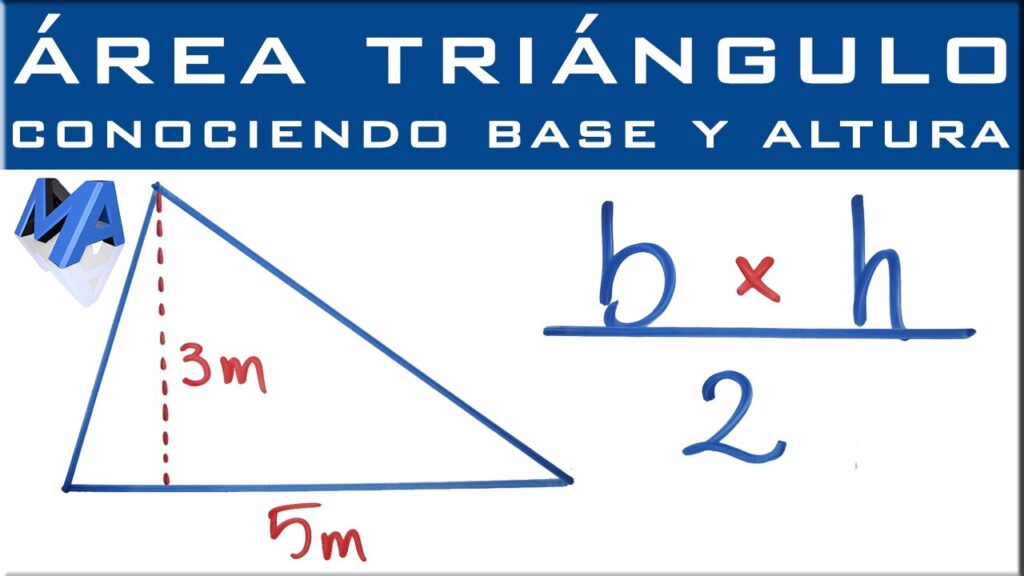
Otra aplicación interesante del Teorema de Pitágoras es en el cálculo de áreas de triángulos rectángulos. Si conocemos las longitudes de los dos catetos, podemos utilizar el teorema para calcular la longitud de la hipotenusa y luego aplicar la fórmula del área de un triángulo (base por altura dividido por dos) utilizando esa hipotenusa como base y uno de los catetos como altura.

El Teorema de Pitágoras es una herramienta matemática que se aplica en numerosos problemas prácticos, tanto relacionados con triángulos rectángulos como en otras situaciones geométricas. Desde el cálculo de longitudes de lados, hasta el cálculo de áreas, este teorema permite resolver problemas de manera precisa y eficiente, ofreciendo una perspectiva fascinante sobre las matemáticas y su aplicabilidad en la vida cotidiana.

Cuáles son algunas de las aplicaciones del Teorema de Pitágoras en la vida cotidiana

El Teorema de Pitágoras es una herramienta matemática fundamental que tiene aplicaciones en diversos campos de la vida cotidiana. A continuación, exploraremos algunas de las principales aplicaciones prácticas de este teorema:

1. Construcción y arquitectura

En el campo de la construcción y la arquitectura, el Teorema de Pitágoras se utiliza para realizar mediciones precisas y asegurar que los ángulos rectos estén correctamente calculados. Por ejemplo, al construir una pared, el teorema nos permite calcular la longitud de la diagonal (hipotenusa) del espacio utilizando las longitudes de los lados (catetos).

Además, el teorema también es esencial para ubicar correctamente las puertas y ventanas en relación con las paredes y el suelo, garantizando así la simetría y estabilidad de la estructura.

2. Geografía e ingeniería civil

En la geografía y la ingeniería civil, el Teorema de Pitágoras se aplica en el cálculo de distancias y alturas. Por ejemplo, al medir una ruta en un mapa, podemos utilizar el teorema para calcular la distancia en línea recta entre dos puntos si conocemos sus coordenadas geográficas.

Asimismo, en la topografía y la cartografía, el teorema es utilizado para determinar alturas y pendientes de terrenos. Esto resulta útil en la planificación de carreteras, puentes y otras infraestructuras.

3. Astronomía y navegación

En la astronomía y la navegación, el Teorema de Pitágoras es utilizado para calcular la distancia entre los astros y la Tierra. Por ejemplo, en la navegación marítima, se utiliza para determinar la posición de un barco en relación con los astros y otros objetos naturales.

Además, el teorema también se aplica en la resolución de problemas relacionados con la óptica astronómica, como el cálculo del tamaño o la distancia de los cuerpos celestes.

4. Electricidad y electrónica

En el campo de la electricidad y la electrónica, el Teorema de Pitágoras es útil para el cálculo de las resistencias en circuitos complejos. Al utilizar el teorema en combinación con las leyes de Ohm, podemos determinar la resistencia total de un circuito cuando hay resistencias conectadas en serie o en paralelo.

También se puede aplicar en el cálculo de la impedancia en circuitos de corriente alterna, lo que resulta esencial en el diseño y funcionamiento de dispositivos electrónicos y sistemas eléctricos.

5. Medicina y biología

Incluso en la medicina y la biología, el Teorema de Pitágoras tiene aplicaciones prácticas. Por ejemplo, se utiliza para determinar la longitud de los huesos en radiografías y para calcular trayectorias de agentes infecciosos en el cuerpo humano.

Además, este teorema también es usado en estudios de anatomía y biomecánica, donde se analizan las fuerzas aplicadas sobre el cuerpo humano y cómo afectan la estructura ósea.

Estas son solo algunas de las numerosas aplicaciones del Teorema de Pitágoras en la vida cotidiana. Sin duda, este teorema ha demostrado ser una herramienta invaluable que trasciende la matemática y nos permite comprender y resolver problemas en diversas áreas del conocimiento humano.

Por qué el Teorema de Pitágoras es considerado uno de los descubrimientos más importantes en la historia de las matemáticas

El Teorema de Pitágoras es ampliamente reconocido como uno de los descubrimientos más importantes en la historia de las matemáticas. Este teorema establece una relación fundamental entre los lados de un triángulo rectángulo y ha sido utilizado durante siglos en una amplia gama de disciplinas, desde la arquitectura hasta la física.

La importancia del Teorema de Pitágoras radica en su capacidad para calcular longitudes desconocidas en triángulos rectángulos. El triángulo rectángulo, como su nombre lo indica, es un triángulo que tiene un ángulo de 90 grados. Esto significa que uno de los ángulos del triángulo es una esquina perfecta. Al establecer una relación precisa entre los sides de este tipo de triángulo, el Teorema de Pitágoras permite a los matemáticos y científicos determinar medidas cruciales sin necesidad de realizar mediciones directas.

Cómo se formula el Teorema de Pitágoras

El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los otros dos lados (las catetos). Matemáticamente expresado:

c^2 = a^2 + b^2

Donde c representa la hipotenusa y a y b representan los catetos del triángulo rectángulo.

Esta fórmula ha sido probada y utilizada en una amplia variedad de contextos matemáticos y prácticos. Desde problemas geométricos hasta cálculos de distancia en navegación, el Teorema de Pitágoras se ha demostrado como una herramienta invaluable para resolver una multitud de problemas.

El origen del Teorema de Pitágoras

El descubrimiento del Teorema de Pitágoras es atribuido al antiguo matemático griego Pitágoras de Samos. Aunque existen evidencias de que los babilonios y egipcios conocían algunos aspectos del teorema mucho antes de Pitágoras, se le atribuye a él la formulación completa y la prueba matemática del mismo.

Pitágoras vivió en el siglo VI a.C. en la isla de Samos, Grecia. Junto con sus seguidores, conocidos como los pitagóricos, realizó investigaciones en diversos campos, incluyendo la música, la astronomía y la geometría. Fue precisamente en esta última disciplina donde su famoso teorema encontró su más fuerte aplicación y desarrollo.

Aunque no se conservan trabajos escritos por Pitágoras, su teorema fue mencionado en textos posteriores y se considera uno de los principales logros de este matemático y filósofo griego.

La influencia del Teorema de Pitágoras en el desarrollo de las matemáticas y en otras áreas del conocimiento continúa siendo relevante hoy en día. Además de su utilidad práctica, este teorema también ha llevado a la formulación de otros teoremas y relaciones matemáticas que han significado avances importantes en diversos campos.

¿Cómo ha cambiado el Teorema de Pitágoras nuestra perspectiva sobre las matemáticas?

El Teorema de Pitágoras es uno de los conceptos matemáticos más famosos y utilizados en todo el mundo. Desde su descubrimiento, ha cambiado drásticamente nuestra perspectiva sobre las matemáticas y ha tenido un impacto significativo en muchas áreas de conocimiento.

No se puede negar que el Teorema de Pitágoras es una de las herramientas fundamentales en geometría euclidiana y trigonometría. Esta simple ecuación nos permite calcular la longitud de uno de los lados de un triángulo rectángulo cuando se conocen los otros dos. Su aplicación se extiende a numerosos campos como la física, la arquitectura, la ingeniería y la computación.

La importancia del Teorema de Pitágoras radica en su capacidad para establecer una relación fundamental entre los lados de un triángulo rectángulo. Esto no solo nos permite realizar cálculos precisos, sino que también revela un aspecto profundo de la naturaleza de las formas geométricas. En este sentido, el teorema tiene un impacto directo en nuestra comprensión de la estructura del espacio y la relación entre las dimensiones.

Incluso más allá de sus aplicaciones prácticas y su influencia en la geometría, el Teorema de Pitágoras ha desafiado nuestra percepción tradicional de las matemáticas. Antes de su descubrimiento, las matemáticas se veían principalmente como una ciencia abstracta y teórica. Sin embargo, el Teorema de Pitágoras demostró que los principios matemáticos podían tener una conexión directa con el mundo físico y tangible.

El Teorema de Pitágoras también ha jugado un papel crucial en la evolución de las matemáticas como disciplina. Su descubrimiento y prueba representaron un avance significativo en la historia de las matemáticas y sentaron las bases para futuros desarrollos. Este hallazgo marcó el comienzo de una nueva era en la comprensión de los principios fundamentales de la geometría y dio lugar a desarrollos posteriores que han sido fundamentales en campos como el cálculo y la teoría de números.

El Teorema de Pitágoras no solo es un concepto fundamental en matemáticas y geometría, sino que también ha cambiado drásticamente nuestra perspectiva sobre el poder y la aplicabilidad de las matemáticas. Su descubrimiento ha tenido un impacto duradero en nuestra comprensión del mundo natural y ha transformado la forma en que abordamos y utilizamos las matemáticas en diversas disciplinas. Sin duda, el origen y la influencia del Teorema de Pitágoras son fascinantes y continúan inspirando a las mentes curiosas en todo el mundo.

Cuáles son algunos otros teoremas o conceptos relacionados con el Teorema de Pitágoras

Además del Teorema de Pitágoras, existen otros teoremas y conceptos relacionados que son fundamentales en la geometría y las matemáticas. Algunos de ellos son:

Triángulo rectángulo:

Un triángulo rectángulo es aquel que posee un ángulo recto, que equivale a 90 grados. En este tipo de triángulos es que se aplica el Teorema de Pitágoras. Los lados que forman el ángulo recto se denominan catetos, mientras que el lado opuesto al ángulo recto se llama hipotenusa.

Identidades trigonométricas:

Las identidades trigonométricas son ecuaciones que relacionan las funciones trigonométricas (seno, coseno y tangente) entre sí. Estas identidades son claves para resolver problemas de trigonometría y también están estrechamente vinculadas con el Teorema de Pitágoras.

Planos cartesianos:

Un plano cartesiano es un sistema de coordenadas compuesto por dos rectas perpendiculares llamadas ejes (X e Y). Este sistema permite representar los puntos en el espacio mediante pares ordenados. La relación entre los ejes y el Teorema de Pitágoras es fundamental para calcular distancias y determinar ubicaciones en el plano.

Fórmula general para resolver polinomios de segundo grado:

La fórmula general para resolver polinomios de segundo grado, también conocida como fórmula de Bhaskara, es un teorema utilizado para encontrar las raíces o soluciones de una ecuación cuadrática. Esta fórmula también tiene una relación directa con el Teorema de Pitágoras, ya que se basa en el discriminante, que se obtiene a partir de los coeficientes de la ecuación cuadrática y utiliza la raíz cuadrada.

Cálculo del área de figuras geométricas:

El Teorema de Pitágoras no solo se aplica al cálculo de las longitudes de los lados de un triángulo rectángulo, sino que también permite calcular el área de diferentes figuras geométricas. Por ejemplo, en un triángulo rectángulo, el área se puede expresar como el producto de los catetos dividido por 2. Este concepto se extiende a otras figuras, como cuadrados, rectángulos y trapecios.

Teorema de Tales:

El Teorema de Tales establece que si trazamos dos rectas paralelas y cortamos ambas con rectas secantes, entonces los segmentos que se forman son proporcionales. Este teorema tiene conexión directa con el Teorema de Pitágoras, ya que se pueden utilizar sus principios para demostrarlo.

Información relacionada:

• <a href="https://www.examplelink.com">Artículo sobre el Teorema de Pitágoras</a>
• <a href="https://www.examplelink.com">Lección de geometría sobre triángulos rectángulos</a>

Se han realizado investigaciones adicionales sobre el Teorema de Pitágoras desde su invención

Desde su invención hace más de 2.000 años, el Teorema de Pitágoras ha sido objeto de numerosas investigaciones y estudios para comprender mejor su origen y aplicaciones. Aunque se atribuye tradicionalmente al matemático griego Pitágoras, existen teorías que sugieren que este famoso teorema pudo haber sido conocido mucho antes de su tiempo.

Una de las teorías más interesantes es la hipótesis de que los antiguos babilonios ya eran conscientes de las relaciones entre los lados de un triángulo rectángulo mucho antes de que Pitágoras naciera. Las tablillas de arcilla encontradas en la antigua Mesopotamia muestran evidencia de cálculos y aproximaciones que se asemejan sorprendentemente al Teorema de Pitágoras.

Además, se han encontrado referencias a nociones similares en antiguas culturas como la egipcia y la india. Estas civilizaciones también tenían conocimientos avanzados sobre geometría y matemáticas, lo que sugiere la posibilidad de que el Teorema de Pitágoras haya sido descubierto de forma independiente en diferentes partes del mundo.

A medida que avanzaba la historia, matemáticos y filósofos como Euclides y Tales de Mileto desarrollaron y expandieron los conceptos relacionados con los triángulos y las relaciones entre sus lados. Estos avances condujeron finalmente a la formulación y consolidación del Teorema de Pitágoras tal como lo conocemos hoy en día.

No obstante, sigue siendo un misterio el proceso exacto de cómo Pitágoras llegó a la conclusión de esta importante relación. Se cree que el propio pitagórico y su escuela mantenían gran parte de sus conocimientos en secreto, lo que complica aún más la tarea de rastrear el origen preciso del teorema.

El Teorema de Pitágoras ha demostrado ser una herramienta fundamental en diversas ramas de las matemáticas y la física, desde la trigonometría hasta la resolución de problemas geométricos. Su simple pero poderosa fórmula permite calcular la longitud de los lados desconocidos de un triángulo rectángulo, a partir de la longitud de los otros dos.

En definitiva, el origen del Teorema de Pitágoras es un tema fascinante que ha capturado la atención de matemáticos e historiadores durante siglos. Aunque su invención se atribuye generalmente a Pitágoras, hay evidencia que sugiere que esta idea podría haber sido conocida incluso antes de su tiempo. Independientemente de su origen, el Teorema de Pitágoras sigue siendo uno de los conceptos fundamentales de las matemáticas y una herramienta indispensable en numerosas aplicaciones prácticas.

Preguntas frecuentes (FAQ)

1. ¿Quién inventó el Teorema de Pitágoras?

El Teorema de Pitágoras no fue inventado por una persona en particular, sino que lleva el nombre del matemático griego Pitágoras debido a su trabajo y contribuciones en el campo de las matemáticas.

2. ¿En qué consiste el Teorema de Pitágoras?

El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los otros dos lados.

3. ¿Cómo se aplica el Teorema de Pitágoras en la vida cotidiana?

El Teorema de Pitágoras es utilizado en diversos campos, como la arquitectura para calcular la longitud de diagonales en planos o la ingeniería para medir distancias y calcular áreas

4. ¿Existen pruebas históricas del Teorema de Pitágoras antes de Pitágoras?

Aunque existen evidencias de que civilizaciones antiguas conocían sobre tripletas pitagóricas, como los babilonios y los chinos, la formulación oficial del teorema se atribuye a Pitágoras y sus seguidores.

5. ¿Por qué el Teorema de Pitágoras es tan importante en las matemáticas?

El Teorema de Pitágoras es importante en las matemáticas porque establece una relación fundamental entre los lados de un triángulo rectángulo, lo cual tiene implicaciones en numerosas áreas, desde la trigonometría hasta la geometría analítica.