Todo lo que debes saber sobre la cardinalidad de un conjunto: descubre cómo contar y medir la cantidad de elementos en un grupo
La cardinalidad de un conjunto es un concepto fundamental en matemáticas que nos permite contar y medir la cantidad de elementos que hay en un grupo o conjunto. Esta propiedad se utiliza en distintas ramas de las matemáticas, como la teoría de conjuntos, el álgebra y la combinatoria. Comprender cómo funciona la cardinalidad es esencial para resolver problemas de conteo y entender las propiedades de los conjuntos.
En este artículo explicaremos en detalle qué es la cardinalidad de un conjunto, cómo se representa y cuáles son sus propiedades más importantes. Veremos ejemplos prácticos para comprender mejor su aplicación y también exploraremos algunas técnicas para calcular o comparar la cardinalidad de dos conjuntos distintos. Además, hablaremos sobre la diferencia entre conjuntos finitos e infinitos, y cómo afecta esto a la forma de determinar su cardinalidad. ¡Sigue leyendo para descubrir todo lo que necesitas saber sobre la cardinalidad de un conjunto!
- Qué es la cardinalidad de un conjunto y por qué es importante
- Cómo se cuenta la cantidad de elementos en un conjunto
- ¿Existen diferentes tipos de cardinalidad? Explora los conceptos de cardinalidad finita e infinita.
- Cuál es la relación entre la cardinalidad y la función de conteo
- Cuáles son las técnicas y métodos utilizados para medir la cardinalidad de conjuntos más grandes
- Cómo se aplica la cardinalidad en situaciones del mundo real, como el recuento de población o el análisis estadístico
- Cuáles son las propiedades y operaciones básicas relacionadas con la cardinalidad de conjuntos
- Cuál es la diferencia entre la cardinalidad y otros conceptos relacionados, como la densidad o la medida de conjuntos
- Qué papel juega la teoría de conjuntos en la comprensión y aplicación de la cardinalidad
- Cómo se relaciona la cardinalidad de un conjunto con temas más avanzados en matemáticas, como la combinatoria o la teoría de números
Qué es la cardinalidad de un conjunto y por qué es importante
La cardinalidad de un conjunto se refiere a la cantidad de elementos que contiene ese conjunto. Es una medida que nos permite contar y medir la cantidad de elementos en un grupo determinado.
La cardinalidad es importante porque nos ayuda a entender las propiedades y características de un conjunto. Al conocer la cantidad de elementos que hay en un conjunto, podemos realizar operaciones matemáticas, como comparar conjuntos, realizar uniones o intersecciones, y calcular probabilidades.
Además, la cardinalidad es fundamental en el estudio de la teoría de conjuntos y la matemática en general. Nos permite establecer relaciones de igualdad, orden y tamaño entre conjuntos, y nos proporciona una base sólida para desarrollar conceptos más avanzados, como conjuntos infinitos.
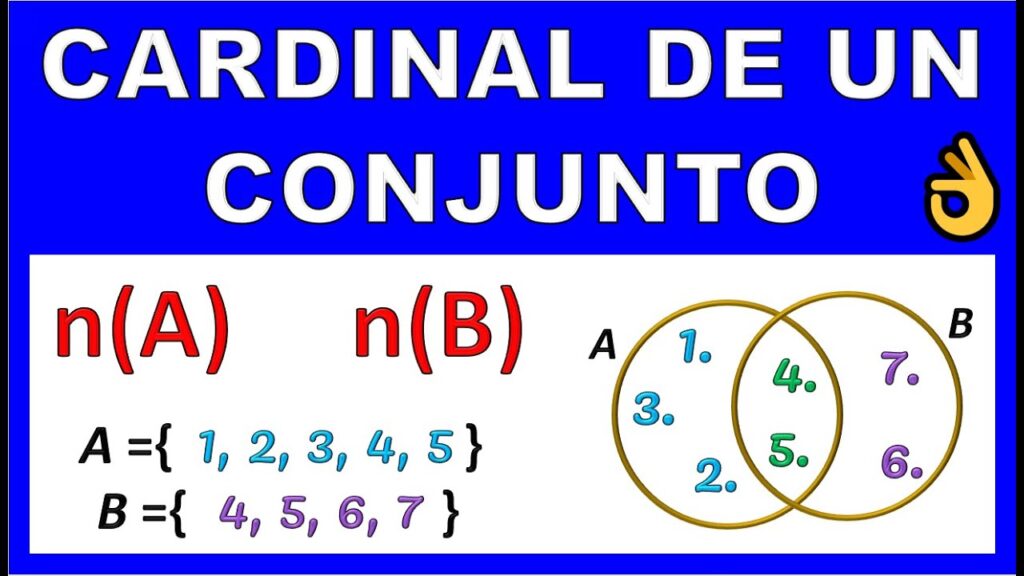
Para determinar la cardinalidad de un conjunto, se utiliza el símbolo "|A|" (donde A representa al conjunto) o el término "n(A)". Estos indican la cantidad de elementos presentes en el conjunto, ya sea finito o infinito.
Es importante tener en cuenta que la cardinalidad de un conjunto no depende del tipo de elementos que lo componen, sino únicamente de la cantidad de elementos presentes. Por ejemplo, un conjunto de números naturales y un conjunto de colores pueden tener la misma cardinalidad si ambos contienen la misma cantidad de elementos.
Cómo contar la cardinalidad de un conjunto finito
Si el conjunto es finito, podemos contar directamente la cantidad de elementos que lo componen. Basta con enumerar cada uno de los elementos y verificar cuántos son en total.
Por ejemplo, si tenemos un conjunto A = {1, 2, 3, 4}, la cardinalidad de A es 4, ya que hay cuatro elementos en el conjunto.
Cómo medir la cardinalidad de un conjunto infinito
Si el conjunto es infinito, no podemos contar los elementos uno por uno. En cambio, utilizamos técnicas más avanzadas para medir su cardinalidad.
Una forma común de medir la cardinalidad de conjuntos infinitos es mediante el uso de correspondencias. Se compara cada elemento del conjunto con otro conjunto que ya conocemos su cardinalidad y se busca una relación de uno a uno entre ambos conjuntos.
Por ejemplo, el conjunto de los números naturales (N) tiene la misma cardinalidad que el conjunto de los números pares (P). Esto se debe a que podemos establecer una correspondencia directa entre ellos: 1 se relaciona con 2, 2 se relaciona con 4, 3 se relaciona con 6, y así sucesivamente. Aunque ambos conjuntos son infinitos, tienen la misma cantidad de elementos, lo que indica que tienen la misma cardinalidad.
Existen diferentes niveles de infinitud en los conjuntos, y es posible comparar la cardinalidad de distintos conjuntos infinitos utilizando herramientas matemáticas como la teoría de conjuntos y la teoría de funciones.
Cómo se cuenta la cantidad de elementos en un conjunto
La cardinalidad de un conjunto se refiere a la medida de la cantidad de elementos que contiene. Para poder contar la cantidad de elementos en un conjunto, es necesario utilizar distintos métodos y técnicas dependiendo del tipo y tamaño del conjunto.
Conjuntos finitos
En el caso de conjuntos finitos, es posible contar directamente la cantidad de elementos utilizando diferentes estrategias. Una opción es emplear el método de conteo uno a uno, donde se asigna a cada elemento del conjunto un número natural consecutivo. Al finalizar este proceso, el último número asignado será exactamente la cantidad de elementos en el conjunto.
Por ejemplo, consideremos el siguiente conjunto:
- {"manzana", "banana", "naranja", "pera"}
Para contar la cantidad de elementos en este conjunto, simplemente asignamos un número a cada elemento:
- {"manzana" (1)}
- {"banana" (2)}
- {"naranja" (3)}
- {"pera" (4)}
En este caso, podemos ver que hay 4 elementos en el conjunto.
Conjuntos infinitos
En el caso de conjuntos infinitos, se utilizan conceptos más complejos para medir su cardinalidad. Un ejemplo de conjunto infinito es el conjunto de los números naturales: {1, 2, 3, 4, ...}. En este caso, no es posible contar todos los elementos de forma directa, ya que se trata de una secuencia infinita.
Para medir la cardinalidad de conjuntos infinitos se utilizan técnicas avanzadas de teoría de conjuntos, como la correspondencia biyectiva con otro conjunto cuya cardinalidad sea conocida. Un ejemplo famoso es el Teorema de Cantor-Bernstein-Schröder, que establece que si existen dos inyecciones entre conjuntos A y B, entonces las cardinalidades de ambos conjuntos son iguales.
La cardinalidad de un conjunto se refiere a la cantidad de elementos que contiene. Para conjuntos finitos se puede utilizar el método de conteo uno a uno, mientras que para conjuntos infinitos se requieren técnicas más avanzadas de teoría de conjuntos.
¿Existen diferentes tipos de cardinalidad? Explora los conceptos de cardinalidad finita e infinita.
La cardinalidad es un concepto fundamental en el estudio de los conjuntos, ya que nos permite determinar la cantidad de elementos que hay en un grupo. Existen diferentes tipos de cardinalidad dependiendo de si el conjunto es finito o infinito.
Cardinalidad finita
Un conjunto se considera finito cuando tiene una cantidad determinada de elementos y es posible contarlos uno por uno. En este caso, la cardinalidad del conjunto se expresa mediante un número natural, que indica exactamente cuántos elementos contiene.
Por ejemplo, si tenemos un conjunto A = {1, 2, 3, 4, 5}, sabemos que tiene 5 elementos y su cardinalidad es 5.
Es importante destacar que la cardinalidad de un conjunto finito siempre será un número natural no negativo. Además, dos conjuntos finitos tienen la misma cardinalidad si y solo si tienen la misma cantidad de elementos.
Cardinalidad infinita
Contrario a los conjuntos finitos, existen conjuntos que poseen una cantidad infinita de elementos. La cardinalidad de un conjunto infinito se representa utilizando símbolos especiales, como ∞ (infinito).
En el caso de los conjuntos infinitos, no se puede contar la cantidad exacta de elementos que contienen. Sin embargo, es posible comparar la cardinalidad de diferentes conjuntos infinitos.
Por ejemplo, el conjunto de todos los números naturales (N) y el conjunto de todos los números enteros (Z) son conjuntos infinitos, pero se puede demostrar matemáticamente que ambos tienen la misma cardinalidad.
También existe una noción de cardinalidad infinita superior, llamada "cardinalidad del continuo". Esta se refiere al conjunto de todos los números reales y tiene una cardinalidad mayor que la de cualquier conjunto contable.
La cardinalidad es un concepto fundamental en la teoría de conjuntos que nos permite contar y medir la cantidad de elementos en un grupo. Puede ser finita o infinita, y existen diferentes niveles de infinitud en los conjuntos.
Cuál es la relación entre la cardinalidad y la función de conteo
La cardinalidad de un conjunto es una propiedad fundamental que nos permite medir la cantidad de elementos que contiene. Esta noción está estrechamente relacionada con la función de conteo, ya que el objetivo principal de esta función es asignar a cada elemento del conjunto un número que represente su posición o índice.
La función de conteo establece una correspondencia entre los elementos del conjunto y los números naturales, de manera que cada elemento se le asigna un número único y cada número está asociado a un único elemento. Esto nos permite llevar a cabo un proceso sistemático de contar y medir la cantidad de elementos en un grupo.
En términos más técnicos, la cardinalidad de un conjunto se define como el número de elementos distintos que contiene. Es importante resaltar que la cardinalidad puede ser finita o infinita, dependiendo de si el conjunto tiene un número limitado o ilimitado de elementos.
Cómo se representa la cardinalidad de un conjunto
Existen diferentes notaciones para representar la cardinalidad de un conjunto. La notación más común es utilizar el símbolo "|A|" para indicar la cardinalidad del conjunto A. Por ejemplo, si tenemos un conjunto A con 5 elementos, escribiríamos |A| = 5.
También es posible representar la cardinalidad de un conjunto utilizando el símbolo #. Siguiendo el mismo ejemplo anterior, podríamos expresar la cardinalidad del conjunto A como #A = 5.
Es importante tener en cuenta que la cardinalidad de un conjunto no depende del orden ni de la repetición de sus elementos. En otras palabras, dos conjuntos pueden tener elementos diferentes pero la misma cardinalidad si la cantidad de elementos en ambos es igual.
Cómo contar elementos en un conjunto
La función de conteo nos permite establecer una correspondencia entre los elementos del conjunto y los números naturales. De esta manera, podemos utilizar los números para llevar a cabo el proceso de contar y determinar la cardinalidad del conjunto.
Existen diferentes estrategias para contar elementos en un conjunto, pero la más común es recurrir a la técnica de contar uno a uno. Esto implica asociar a cada elemento del conjunto un número natural de manera secuencial, comenzando desde el número 1 hasta llegar al último elemento.
Por ejemplo, supongamos que tenemos un conjunto A = {manzana, banana, naranja}. Para contar los elementos en este conjunto, asignaríamos el número 1 a la manzana, el número 2 a la banana y el número 3 a la naranja.
También es posible utilizar la función de conteo para verificar si dos conjuntos tienen la misma cardinalidad. En este caso, simplemente contaríamos los elementos de cada conjunto y compararíamos los resultados. Si ambos conjuntos tienen la misma cantidad de elementos, diremos que tienen la misma cardinalidad; de lo contrario, diremos que tienen cardinalidades diferentes.
Cuáles son las técnicas y métodos utilizados para medir la cardinalidad de conjuntos más grandes
Para medir la cardinalidad de conjuntos más grandes, existen diferentes técnicas y métodos que se pueden utilizar. A continuación, mencionaremos algunos de los más comunes:
1. Método de conteo directo:
Este método consiste en contar uno a uno los elementos del conjunto para determinar su cardinalidad. Es una técnica simple y directa que se utiliza cuando el conjunto no es muy grande. Por ejemplo, si tenemos un conjunto de frutas como manzanas, naranjas y plátanos, podemos contar cuántas hay de cada uno.
2. Uso de tablas o matrices:
Otra forma de medir la cardinalidad de un conjunto es utilizando tablas o matrices. En una tabla o matriz, se pueden organizar los elementos del conjunto en filas y columnas, asignando una celda para cada combinación de elementos. Luego, se puede contar la cantidad de celdas ocupadas para obtener la cardinalidad del conjunto.
3. Método de muestreo:
Este método consiste en seleccionar una muestra representativa del conjunto y contar los elementos de la muestra. Luego, se utiliza esta información para hacer una estimación de la cardinalidad total del conjunto. Este método es útil cuando el conjunto es muy grande y contar todos los elementos sería impracticable.
4. Uso de fórmulas matemáticas:
En algunos casos, es posible utilizar fórmulas matemáticas para calcular la cardinalidad de un conjunto. Por ejemplo, si se conoce el número de elementos totales y la proporción de elementos que cumplen cierta condición, se puede utilizar una fórmula de proporción para obtener la cardinalidad.
5. Uso de algoritmos de conteo:
En conjuntos muy grandes o complejos, puede ser necesario utilizar algoritmos de conteo para determinar su cardinalidad. Estos algoritmos utilizan técnicas avanzadas como el muestreo aleatorio y el análisis combinatorio para realizar el conteo de manera eficiente.
Existen diferentes técnicas y métodos que se pueden utilizar para medir la cardinalidad de conjuntos más grandes. La elección del método dependerá de la naturaleza del conjunto y de los recursos disponibles. Es importante seleccionar el método adecuado para obtener resultados precisos y confiables.
Cómo se aplica la cardinalidad en situaciones del mundo real, como el recuento de población o el análisis estadístico
La cardinalidad es un concepto fundamental en las matemáticas que nos permite contar y medir la cantidad de elementos en un conjunto. Aunque a primera vista pueda parecer abstracto o solo aplicable en el ámbito teórico, la verdad es que la cardinalidad tiene muchas aplicaciones en situaciones del mundo real.
Una de las aplicaciones más evidentes de la cardinalidad es en el recuento de población. En un censo o estudio demográfico, es necesario saber cuántas personas viven en una determinada área geográfica. Para hacer esto, se utiliza la cardinalidad para contar individualmente cada uno de los habitantes y obtener una cifra precisa y confiable que refleje la cantidad de personas que componen esa población.
Además del recuento de población, la cardinalidad también se aplica en el análisis estadístico. En este campo, es común trabajar con conjuntos de datos que contienen información sobre diferentes variables. Por ejemplo, en un estudio médico se podrían analizar los resultados de pruebas de laboratorio para determinar la relación entre ciertos factores y la presencia de una enfermedad. Aquí, la cardinalidad es utilizada para contar la cantidad de registros en el conjunto de datos y así poder realizar cálculos estadísticos como promedios, desviaciones estándar y correlaciones.
Otra aplicación interesante de la cardinalidad es en el diseño de bases de datos. En este contexto, la cardinalidad se utiliza para describir la relación entre tablas y entender cómo se relacionan los registros en cada una de ellas. Por ejemplo, en una base de datos de una tienda en línea, se podrían tener dos tablas: una con información de los productos y otra con información de los clientes. La cardinalidad ayuda a determinar si la relación entre estas dos tablas es de uno a muchos, muchos a muchos o uno a uno, lo cual es clave para el diseño eficiente de la base de datos.
La cardinalidad no es solo un concepto abstracto de las matemáticas, sino que tiene muchas aplicaciones prácticas en situaciones del mundo real. Ya sea en el recuento de población, el análisis estadístico o el diseño de bases de datos, la cardinalidad nos permite contar y medir la cantidad de elementos en un conjunto, brindándonos información valiosa para tomar decisiones y entender mejor el entorno que nos rodea.
Cuáles son las propiedades y operaciones básicas relacionadas con la cardinalidad de conjuntos
La cardinalidad de un conjunto es una propiedad importante que nos permite medir la cantidad de elementos que contiene dicho conjunto. En matemáticas, se representa con el símbolo '|A|', donde 'A' es el conjunto en cuestión.
Propiedades de la cardinalidad:
- La cardinalidad de un conjunto siempre es un número no negativo.
- Si un conjunto tiene una cantidad finita de elementos, su cardinalidad será un número natural.
- Si un conjunto no tiene elementos, se dice que es un conjunto vacío y su cardinalidad es igual a cero.
- La cardinalidad de un conjunto no depende del orden o la forma de presentar los elementos del conjunto.
- Para dos conjuntos A y B, si A y B tienen la misma cantidad de elementos, se dice que tienen la misma cardinalidad y se denota como |A| = |B|.
Operaciones básicas relacionadas con la cardinalidad:
Existen varias operaciones que podemos realizar utilizando la cardinalidad de conjuntos:
- Unión: La cardinalidad de la unión de dos conjuntos A y B se calcula sumando las cardinalidades individuales y restando la intersección de ambos conjuntos.
- Intersección: La cardinalidad de la intersección de dos conjuntos A y B se calcula restando las cardinalidades individuales y sumando la unión de ambos conjuntos.
- Diferencia: La cardinalidad de la diferencia A - B entre dos conjuntos A y B se calcula restando la cardinalidad de B a la cardinalidad de A.
- Conjunto complemento: Si tenemos un conjunto universal U y un conjunto A contenido en U, la cardinalidad del complemento de A (A') se calcula restando la cardinalidad de A a la cardinalidad de U.
|A ∪ B| = |A| + |B| - |A ∩ B|
|A ∩ B| = |A| + |B| - |A ∪ B|
|A - B| = |A| - |B|
|A'| = |U| - |A|
Estas propiedades y operaciones básicas son fundamentales para manipular la cardinalidad de conjuntos y realizar cálculos precisos en diversas situaciones matemáticas.
Cuál es la diferencia entre la cardinalidad y otros conceptos relacionados, como la densidad o la medida de conjuntos
La cardinalidad de un conjunto se refiere a la cantidad de elementos que tiene ese conjunto. Es una medida absoluta de la cantidad de elementos presentes en un grupo determinado.
Por otro lado, la densidad de un conjunto se refiere a la distribución de los elementos dentro del conjunto en relación con algún contexto específico. Por ejemplo, en el caso de una distribución espacial, la densidad de un conjunto puede referirse a qué tan cercanos están los elementos entre sí en términos de distancia.
La medida de conjuntos, por su parte, es una noción más general que abarca tanto la cardinalidad como la densidad, así como otras medidas que pueden ser utilizadas para caracterizar los conjuntos, como la dimensión fractal o la probabilidad de ocurrencia de ciertos eventos dentro del conjunto.
La cardinalidad se centra en contar la cantidad de elementos en un conjunto, mientras que la densidad se enfoca en la distribución espacial o contextual de esos elementos. La medida de conjuntos engloba ambas nociones y puede incluir otras medidas relacionadas con la estructura o propiedades del conjunto.
Qué papel juega la teoría de conjuntos en la comprensión y aplicación de la cardinalidad
La teoría de conjuntos desempeña un papel fundamental en la comprensión y aplicación de la cardinalidad de un conjunto. La cardinalidad es una medida que nos permite contar y medir la cantidad de elementos dentro de un grupo o conjunto.
En matemáticas, un conjunto es una colección de objetos, los cuales pueden ser números, letras, elementos abstractos, entre otros. La cardinalidad nos ayuda a determinar cuántos elementos hay en ese conjunto, es decir, su tamaño o magnitud.
Para representar la cardinalidad de un conjunto, se utiliza la notación |A|, donde A es el conjunto en cuestión. Por ejemplo, si tenemos un conjunto A = {1, 2, 3}, su cardinalidad se representa como |A| = 3, ya que contiene tres elementos.
La cardinalidad de un conjunto tiene diversas aplicaciones y utilidades en diferentes áreas de estudio. En la estadística, por ejemplo, la cardinalidad permite medir la frecuencia de un evento o suceso en una muestra o población. En la teoría de conjuntos, la cardinalidad es esencial para comparar y clasificar conjuntos según su tamaño.
Es importante destacar que la cardinalidad no está limitada solo a conjuntos finitos, sino que también se puede aplicar a conjuntos infinitos. En este caso, la cardinalidad se mide utilizando conceptos más avanzados, como los números cardinales transfinitos.
Para calcular la cardinalidad de un conjunto, simplemente se cuentan todos los elementos que lo conforman. Sin embargo, existen algunos casos especiales donde la cardinalidad puede ser infinita o indeterminada. Estos casos suelen presentarse en conjuntos con propiedades particulares, como los conjuntos no numerables o los conjuntos vacíos.
La teoría de conjuntos nos permite comprender y aplicar la cardinalidad de un conjunto, una medida esencial para contar y medir la cantidad de elementos en un grupo. La cardinalidad tiene múltiples usos en diversas áreas de estudio y puede ser aplicada a conjuntos finitos e infinitos. Es importante conocer las propiedades y peculiaridades de la cardinalidad para realizar cálculos precisos y obtener resultados sólidos en diferentes problemas matemáticos.
Cómo se relaciona la cardinalidad de un conjunto con temas más avanzados en matemáticas, como la combinatoria o la teoría de números
La cardinalidad de un conjunto no solo es un concepto fundamental en matemáticas elementales, sino que también se relaciona directamente con temas más avanzados y complejos, como la combinatoria o la teoría de números.
En la combinatoria, por ejemplo, se utilizan técnicas de conteo que se basan en la cardinalidad de los conjuntos. A través de fórmulas y principios combinatorios, es posible determinar la cantidad de posibles combinaciones, variaciones o permutaciones que se pueden formar a partir de un conjunto dado. Estos cálculos permiten resolver problemas relacionados con la distribución de objetos, el conteo de casos favorables en probabilidad y otros aspectos de la teoría combinatoria.
Por su parte, la teoría de números también utiliza conceptos de la cardinalidad de conjuntos para analizar las propiedades y comportamientos de los números. Por ejemplo, uno de los problemas clásicos de esta rama de las matemáticas es intentar contar la cantidad de números primos existentes. Aquí, se utilizan técnicas que involucran la cardinalidad de los conjuntos de manera indirecta, ya que se exploran las características de los números compuestos para determinar la presencia de números primos.
Asimismo, la cardinalidad de conjuntos es relevante en otras áreas de las matemáticas más avanzadas, como el análisis combinatorio, la teoría de conjuntos aplicada a la computación y la teoría de modelos. En cada una de estas disciplinas, se emplean métodos y herramientas específicas que tienen como base la noción de cardinalidad para resolver problemas complejos y profundizar en el estudio de distintos fenómenos matemáticos.
La cardinalidad de un conjunto es el número de elementos que contiene.
Para contar la cardinalidad de un conjunto, se cuentan uno a uno los elementos y se obtiene el total.
Un conjunto es finito cuando tiene un número determinado de elementos, que no es infinito.
Un conjunto es infinito cuando no se puede contar todos sus elementos, ya que son innumerables.
Sí, un conjunto puede tener cardinalidad cero si no tiene ningún elemento.
Deja una respuesta
Entradas relacionadas